8√3
Объяснение:
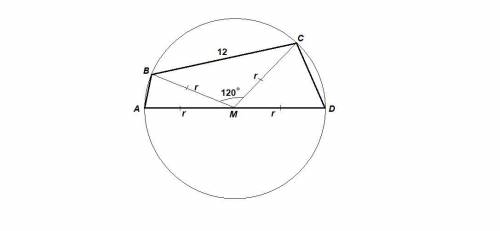
MA = MB = MC = MD, значит М - центр описанной около четырехугольника окружности.
Если четырехугольник вписан в окружность, то суммы противолежащих углов равны 180°.
∠А = 180° - ∠С = 180° - 95° = 85°
∠D = 180° - ∠B = 180° - 115° = 65°
ΔАВМ равнобедренный, значит углы при основании АВ равны, ⇒
∠АМВ = 180° - 2∠А = 180° - 2 · 85° = 180° - 170° = 10°
ΔMCD равнобедренный, значит углы при основании CD равны, ⇒
∠CМD = 180° - 2∠D = 180° - 2 · 65° = 180° - 130° = 50°
∠ВМС = 180° - (∠АМВ + ∠CМD) = 180° - 60° = 120°
ΔВМС: по теореме косинусов:
BC² = MB² + MC² - 2·MB·MC·cos120°
144 = r² + r² - 2 · r · r · (-1/2)
144 = 2r² + r²
3r² = 144
r² = 48
r = 4√3
AD = 2r = 8√3
20cм
Объяснение:
Проводим диагональ САD.
∠САD = ∠АСВ = 45° - как накрест лежащие углы.
∠ВАС = ∠АСВ= 90 - 45 =45°
Δ АВС получается равнобедренный, а это значит АВ = ВС = 10 см
АК = ВС = 10 см
Так как АК : КD = 1 : 2 , то
КD = 10 * 2 = 20 см
Теперь находим большее основание трапеции
АD = АК + КD = 10 + 20 = 30 см.
Среднюю линию обозначим МN
МН = (ВС + АD )\ 2 = (10 +30 ) \ 2 = 20 см