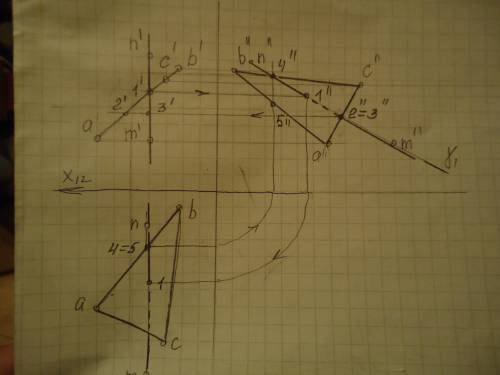
ответ: Построение точки пересечения см. на фото.
Объяснение:
Задание относится к "Начертательной геометрии".
Постройте профильные проекции прямой и треугольника.
Точка 1¹- проекция точки пересечения прямой и плоскости на виде спереди. Найдите проекцию 1¹¹ на виде слева.
Для того, чтобы определить видимость на виде слева, выберем совпадающие точки 2¹¹ и 3¹¹. Получив точки 2¹ и 3¹, видим,что треугольник к наблюдателю ближе, чем прямая. Видимость на виде слева определена.
Найдём проекцию 1 на виде сверху. На виде сверху возьмём совпадающие точки 4 и 5. Найдём их проекции на виде слева: 4¹¹ и 5¹¹. Видя, что 4¹¹, принадлежащая прямой, находится выше, чем 5¹¹ на а¹¹b¹¹, получаем, что на виде сверху в этом месте видна прямая.
Надеюсь, что смогла вам
1) апофема равна 3
2) площадь нижнего основания равно 81см²
3) площадь верхнего основания равно 1см²
4) площадь боковой поверхности 60см²
5) площадь полной поверхности 142см²
Объяснение:
MP=A'D'=1см
AM=(AD-MP)/2=(9-1)/2=8/2=4см
Теорема Пифагора
А'М=√(АА'²-АМ²)=√(5²-4²)=3см. апофема
Sбок=4*АМ(А'D'+AD)/2=4*3(1+9)/2=
=12*10/2=60см²
Sосн'=А'В'²=1²=1см²
Sосн=АВ²=9²=81см²
Sпол=Sосн'+Sосн+Sбок=60+81+1=142см²
Хотелось найти апофему через высоту пирамиды.
АС=АВ√2=9√2см
А'С'=А'В'√2=1√2см.
НК=А'С'=√2см.
АН=(АС-НК)/2=√(9√2-√2)/2=4√2
∆АА'Н- прямоугольный треугольник
Теорема Пифагора
А'Н=√(АА'²-АН²)=√(5²-(4√2)²)=√(25-32)
Условие не корректно.
Нет высоты, нет апофемы, нет площади боковой поверхности, нет площади полной поверхности.



32,9
Объяснение:
Если EC-32,9 , а мендиана идет на середину , то ВЕ будет 32,9