68. По данным на рисунке найдите площадь 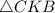 .
.
ΔСКВ - прямоугольный (∠С = 90°).
СК - высота (СК⊥АВ).
АК = 4, КВ = 16.
Найти :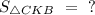 Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.
Решение :В прямоугольном треугольнике высота, проведённая к гипотенузе - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 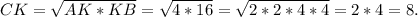
Следовательно, 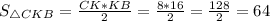 ед².
ед².
64 ед².
- - -70. ABCD - прямоугольник. Найдите 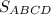 .
.
Четырёхугольник ABCD - прямоугольник.
АС - диагональ.
HD⊥АС.
HD = 6, АН = 9.
Найти :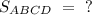
Следовательно ∠D = 90°.
Рассмотрим ΔACD - прямоугольный.
В прямоугольном треугольнике высота, опущенная на гипотенузу - это среднее геометрическое между отрезками, на которое поделило основание высоты гипотенузу.Следовательно, 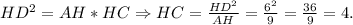
Следовательно, 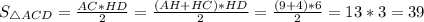 ед².
ед².
Тогда 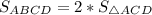 = 2*39 ед² = 78 ед².
= 2*39 ед² = 78 ед².
78 ед².
Если мы продлим радиус OA до точки пересечения с окружностью с радиусом OB (пусть он пересекает эту окружность в точке C), то A окажется средней точкой OC, потому что радиус OA = 2, а радиус OC = 4. OC/2 = 4/2 = 2. Значит, AB - медиана треугольника ACO. OB = OC, потому что это радиусы большей окружности. Значит, треугольник BCO равнобедренный, поэтому углы при основании равны. Сумма углов треугольника равна 180, а третий угл нам дан по условию. Найдём два оставшихся.
x = (180 - 60)/2 = 120/2 = 60
Значит все углы по 60 градусов, значит, треугольник равносторонний, значит медиана AB также является биссектрисой и высотой, значит, ABO - прямоугольный треугольник с прямым углом B, значит, мы можем найти AB по теореме Пифагора:
AB = √(OB^2 - AO^2)
AB = √(4^2 - 2^2)
AB = √(16 - 4)
AB = √(12)
AB = √(4 * 3)
AB = 2√3