S бок = 2пRh = п(2 * 4 * 7) = 56п см²
S полн поверхности = 2пR(R + h) = п(8 * 4 + 8 * 7) = 88п см²
ответ: 56п см², 88п см²
(к 1 задаче рисунка нет)
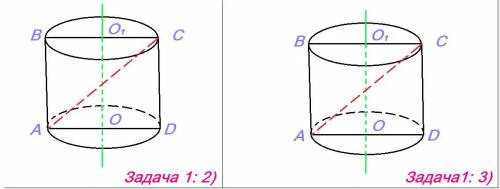
Задача 1: 2)Так как h (на рисунке ОО1) = 8 см => АВ = CD = h = 8 см
D = 2R = 3 * 2 = 6 см => ВС = AD = D = 6 см
Найдём АС, по теореме Пифагора:
с² = а² + b²
c = √(a² + b²) = √(6² + 8²) = √(36 + 64) = √100 = 10 см
ответ: 10 см.
Задача 1: 3)S бок = 0,5S полн поверхности, по условию.
S полн поверхности = 2S осн + S бок
2S бок = 2S осн+ S бок
S бок = 2S осн
2пRh = 2пR²
h = R
АС = 5 см, по условию.
Найдём радиус R, по теореме Пифагора, а именно составим уравнение:
с² = а² + b²
АС² = CD² + AD²
5² = R² + (2R)²
25 = 5R²
5 = R²
R = √5
Итак, R = √5 см
Мы узнали, что h = R => h = √5 см
=> S полн поверхность = 2пR(R + h) = 2п√(5)(√(5) + √(5)) = 20п см²
ответ: 20п см²
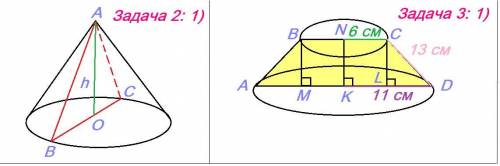
-------------------------------------2. Конус.Задача 2: 1)R = D/2 = 24/2 = 12 см
S бок = пRl = п(12 * 13) = 156п см²
S полн поверхности = S осн + S бок = пR² + пRl = 144п + 156п = 300п см²
Найдём h, по теореме Пифагора:
с² = а² + b²
a = √(c² - b²) = √(13² - 12²) = √(169 - 144) = √25 = 5 см
Итак, h = 5 см
ответ: 5см, 300п см², 156п см²
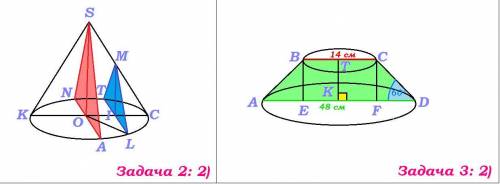
Задача 2: 2)Осевое сечение конуса (если ось плоскость проходит через ось конуса) - равнобедренный треугольник, а высота SO делит этот равнобедренный треугольник на два равных прямоугольных треугольника KSO и CSO(их равенство можно доказать по всем признакам равенства прямоугольных треугольников, исходя из того, что △KSC - равнобедренный)
Итак, △KSC - осевое сечение этого конуса.
SO - высота конуса.
MI - высота сечения, параллельного осевому.
△MCI подобен △SCO с коэффициентом подобия k = IC/OC
IC = OC - OI = 6 - 2 = 4 см
Итак, k = 4/6 = 2/3
MI = SO * k = 12 * 2/3 = 8 см
Рассмотрим △OIL:
OL = 6 см - радиус основания конуса.
OI = 2 см, по условию.
Найдём IL, по теореме Пифагора:
с² = а² + b²
a = √(c² - b²) = √(6² - 2²) = √(36 - 4) = √32 = 4√2 см
S△LMT = 1/2MI * LT = IL * MI = 4√2 * 8 = 32√2 см²
ответ: 32√2 см²
-------------------------------------3. Усечённый конус.Задача 3: 1)NC = 6 см, по условию. (r)
KD = 11 см, по условию.(R)
LD = KD - NC = 11 - 6 = 5 см
Найдём высоту CL, по теореме Пифагора:
с² = а² + b²
a = √(c² - b²) = √(13² - 5²) = √(169 - 25) = √144 = 12 см
Итак, CL = 12 см
S бок = п(R + r) * l = (6 + 11) * 13 = 221п см²
S полн поверхности = п(R + r) * l + пR² + пr² = п(11 + 6) * 13 + п(11)² + п(6)² = 378п см²
ответ: 12 см, 221п см², 378п см².
Задача 3: 2)D = ВС = 14 см, по условию.
D = AD = 48 см, по условию.
R = BT = TC = D/2 = 14/2 = 7 см
R = AK = KD = D/2 = 48/2 = 24 см
TC = 7 см (r)
KD = 24 см (R)
FD = KD - TC = 24 - 7 = 17 см
Рассмотрим △FCD:
он прямоугольный, так как CF - высота..
Сумма острых углов прямоугольного треугольника равна 90°
=> ∠FCD = 90˚ - 60˚ = 30˚
Если угол прямоугольного треугольника равен 30°, то напротив лежащий катет равен половине гипотенузы.
=> CD = 17 * 2 = 34 см
S бок = п(R + r) * l = п(24 + 7) * 34 = 1054п см²
ответ: 1054п см² .
Площадь S1 боковой поверхности призмы равна произведению периметра перпендикулярного сечения призмы на её боковое ребро. Плоскость перпендикулярного сечения пересекает боковые грани по их высотам. Поэтому периметр перпендикулярного сечения равен сумме этих высот, т. е. 3*2=6.
Значит, S1 = 3al = 18
ПустьS -- площадь основания призмы. Площадь ортогональной проекции основания призмы на плоскость, перпендикулярную боковым рёбрам, равна площади перпендикулярного сечения, делённой на косинус угла между плоскостями основания и перпендикулярного сечения. Этот угол равен углу между боковым ребром и высотой призмы, т. е. 60∘.
Поэтому
S2= 2√3Следовательно, площадь полной поверхности призмы равна