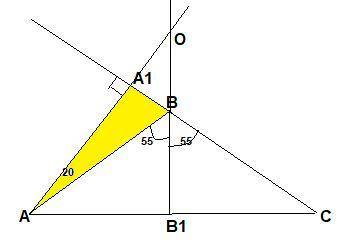
В равнобедренном треугольнике ABC угол B равен 110 градусов. Определите угол между прямой, содержащей высоту AA1, и прямой, содержащей биссектрису BB1. ответ запишите в градусах.
Объяснение:
Высота АА₁ падает на продолжение стороны ВС, т.к ∠АВС тупой. Тогда углом между между прямой, содержащей высоту AA₁, и прямой, содержащей биссектрису BB₁ будет∠АОВ₁ .
Угол АВС внешний для Δ АВА₁, значит ∠ВАА₁=110°-90°=20°.
ΔАВС-равнобедренный, углы при основании равны
∠ВАС=(180-110°):2=35° → ∠В₁АО=35°+20°=55°.
Δ АОВ₁ -прямоугольный , ∠АОВ₁=90°-55°=35°
1. Дополнительное построение: проведём DH- высоту
2.Так как AB=CD, то
Δbdc- равнобедренный, отсюда BH медиана (по свойству р/б треугольника)
3. BH=HC=31/2=15,5
4. ∠CDH=180°-90°-45°=45°, ΔCDH- равнобедренный. CH=HD=15,5
5. Sabcd=BC*HD=31*15,5=480,5
ответ: Sabcd=480,5