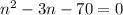
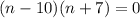
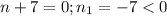 - не подходит, количество вершин не может быть отрицательным
- не подходит, количество вершин не может быть отрицательным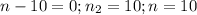
Допусти, что скорость 1-го бегуна = Х км/ч,
тогда скорость 2-го бегуна = Х+5 км/ч
Поскольку в задании сказано, что "Спустя один час, когда
первому из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун первый круг 15 минут назад", значит 2-й бегун пробежал первый круг за время = 1 час - 15 минут = 45 минут
45 минут = 45/60 = 0,75 часа
Длина круга = скорость бегуна * время, которое потрачено на преодоление одного круга.
Поэтому Длина круга = скорость 1-го бегуна * время, которое потрачено на преодоление одного круга 1-м бегуном = (Х+5) * 0,75= 0,75Х + 3,75
Поскольку в задании сказано, что "Спустя один час, когда
первому из них оставалось 1 км до окончания первого круга..."
Значит Длина круга = скорость 2-го бегуна * время, которое потрачено 2-м бегуном + 1 км, который оставался до окончания первого круга= Х * 1 +1 = Х+1
Поэтому сможем составить уравнение:
0,75Х + 3,75 = Х+1
Х-0,75Х = 3,75-1
0,25Х = 2,75
Х=2,75/0,25
Х=11 - это скорость 1-го бегуна
Тогда скорость 2-го бегуна = Х+5 = 11+5=16 км/ч
ответ: скорость 2-го бегуна = 16км/ч
ответ:
image
на сторонах угла∡abc точки a и c находятся в равных расстояниях от вершины угла ba=bc. через эти точки к сторонам угла проведены перпендикуляры ae⊥ba cd⊥bc.
1. чтобы доказать равенство δafd и δcfe, докажем, что δbae и δbcd, по второму признаку равенства треугольников:
ba=bc
∡baf=∡bcf=90°
∡abc — общий.
в этих треугольниках равны все соответсвующие эелементы, в том числе bd=be, ∡d=∡e.
если bd=be и ba=bc, то bd−ba=be−bc, то есть ad=ce.
очевидно равенство δafd и δcfe также доказываем по второму признаку равенства треугольников:
ad=ce
∡daf=∡ecf=90°
∡d=∡
объяснение: