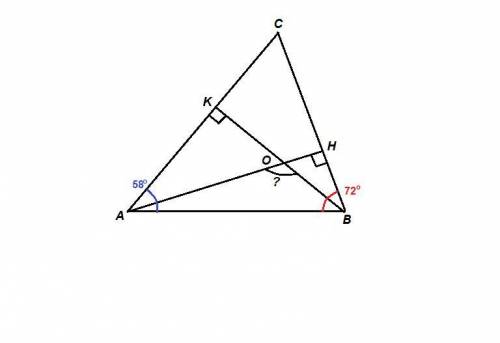
130°
Объяснение:
Сумма острых углов прямоугольного треугольника равна 90°.
ΔАНВ: ∠ АНВ = 90°,
∠ВАН = 90° - ∠АВН = 90° - 72° = 18°
ΔВКА: ∠ВКА = 90°,
∠АВК = 90° - ∠ВАК = 90° - 58° = 32°
ΔАОВ:
∠АОВ = 180° - (∠ВАО + ∠АВО) = 180° - (18° + 32°) =
= 180° - 50° = 130°
Из ΔАВС:
∠С = 180° - (∠А + ∠В) = 180° - (58° + 72°) = 180° - 130° = 50°
Сумма углов выпуклого четырехугольника равна 360°.
Для четырехугольника СКОН:
∠КОН = 360° - (∠С + ∠К + ∠Н) = 360° - (50° + 90° + 90°) =
= 360° - 230° = 130°
Дано: прямоугольный треугольник АВС;
угол С = 90;
СА = 3;
СВ = 4;
СН - высота.
Найти: СН - ?
1) рассмотрим прямоугольный треугольник АВС. Тогда по теореме Пифагора:
АС^2 + СВ^2 = АВ^2;
3^2 + 4^2 = АВ^2;
9 + 16 = АВ^2;
25 = АВ^2;
АВ = 5;
2) В прямоугольном треугольнике каждый катет - это среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу. Тогда
ВС = √( АВ * НВ);
4 = √( 5 * НВ) (возведем правую и левую часть в квадрат);
16 = 5 * НВ;
НВ = 16/5;
НВ = 3,2;
3) АС = √( АВ * НА);
3 = √( 5 * НА) (возведем правую и левую часть в квадрат);
9 = 5 * НА;
НА = 9/5;
НА = 1,8;
4) СН = √АН * НВ;
СН = √1,8 * 3,2;
СН = √5,76;
СН = 2,4.
ответ: 2,4.