Линия пересечения плоскости AD₁C₁ и плоскости основания есть ребро параллелепипеда АВ.
Угол между плоскостью AD₁C₁ и плоскостью основания есть угол между плоскостью AD₁C₁ перпендикуляром к АВ, то есть высотой ромба. На рисунке обозначена как ВН.
ΔСВН - прямоугольный, с прямым углом Н, по условию острый угол ромба-основания равен 60⁰, отсюда, зная sin60⁰ находим высоту ромба ВН:
а) 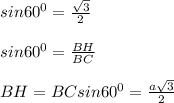
Можно было вычислить и так, как мы находили АН во вчерашнем задании, через т. Пифагора, зная, что СН=а/2, как катет, лежащий против угла в 30⁰, но сегодня решаем так, чтобы показать разные пути решения.
б) Высоту параллелепипеда HH₁находим из прямоугольного ΔВН₁Н в котором угол Н прямой, угол В=60⁰, и зная значение tg60⁰:
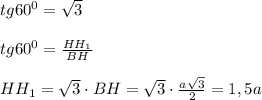
в) Найти площадь боковой поверхности - самая простая часть этого задания:
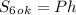 , где
, где 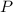 и
и  - периметр основания и высота пераллелепипеда соответственно.
- периметр основания и высота пераллелепипеда соответственно.

г) 
Дано: треугольник АВС, АВ = 18 см, ВС:АС=5:6
Доказать: Угол В равен углу С.
Доказательство:
1) Пусть длина стороны ВС = 5х см, тогда длина стороны АС = 6х см.
Р = АВ+ВС+АС = 18+5х+6х = 18+11х
18+11х = 51
11х = 33
х = 3, отсюда ВС = 15 см, АС = 18 см.
Таким образом, AC = AB = 18 см, следовательно, треугольник АВС - равнобедренный. По свойству равнобедренного треугольника, углы при основании равны, значит угол В равен углу С, что и требовалось доказать.