1 вариант
1) Сумма всех углов прямоугольного треугольника 180°, следовательно угол А = 180-90-43 = 47°
2) Катет лежащий на против угла в 30° градусов равен половине гипотенузы СВ = АВ/2 = 12см
3) Катет лежащий на против угла в 30° градусов равен половине гипотенузы угол М = 30°, следовательно KL = КМ/2 = 9 см
4) Находим катет ВС по теореме Пифагора
Находим синус угла А, sin(A) = 13,85/16 = 0,865625
Угол А будет равен арксинусу этого числа 59,95 можно округлить до 60°.
5) В треугольнике угол MNO будет равен 30°, поскольку в треугольник MNK прямоугольный. Гипотенуза MN будет равно 6, так как катет МО лежит на против угла в 30°, а значит он равен половине гипотенузы. Катет NO находим по теореме Пифагора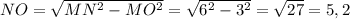 
. В прямоугольном треугольнике NOK катет NO лежит на против угла в 30°, значит он равен половине гипотенузы, следовательно гипотенуза NK = 10,4. Катет ОК находим по теореме Пифагора ОК = 9,0066 округлим до 9. МК = МО + ОК = 12.
2 Вариант
1) Сумма всех углов прямоугольного треугольника равна 180°, следовательно угол К будет равен К = 180 - 90 - 72 = 18°.
2) Катет ВС лежит на против угла А, который равен 30°, следовательно катет равен половине гипотенузы 15 см.
3) Катет XZ лежит на против угла в 30° он равен половине гипотенузы, следовательно гипотенуза XY = 2*XZ = 24.
4) Находим катет АС по теореме Пифагора. АС = 36,4. Находим синус угла В, sin(B) = 36,4/42 = 0,8666. Угол В будет равен арксинусу этого числа. Угол В равен 60,07° можно округлить до 60°
5) В прямоугольном треугольнике АВС, катет АС лежит на против угла в 30°, следовательно он равен половине гипотенузы АВ, катет АС = 40 см. В треугольнике МСВ угол МСВ равен 60°, поскольку в этом треугольнике угол СМВ прямой. Следовательно угол АСМ = 90-60 = 30°. В треугольнике АСМ катет АМ лежит на против угла в 30° и он равен половине от гипотенузы АС, следовательно катет АМ = 20см.
ответ:Если голуби, стартовавшие синхронно и с одинаковой скоростью, долетели до зерна одновременно, значит, образованные фонарем, домом, землей и траекторией полета голубей два прямоугольных треугольника будут иметь равные гипотенузы (траектории полета голубей).
У одного треугольника катеты будут соответственно равны высоте дома (15 м) и отрезку земли до места, где Анна рассыпала зерно, обозначим его Х м.
У другого треугольника катеты будут соответственно равны высоте фонарного столба (8 м) и отрезку земли до места, где Анна рассыпала зерно:
23 - Х м.
Так как гипотенузы треугольников равны, то на основании теоремы Пифагора, согласно которому квадрат гипотенузы равен квадрату катетов, можно составить уравнение:
с2 = 152 + Х2 = 82 + (23 – Х) 2;
152 + Х2 = 82 + 232 – 2 * 23 * Х + Х2;
152 + Х2 = 82 + 232 – 2 * 23 * Х + Х2;
152 = 82 + 232 – 2 * 23 * Х;
225 = 64 + 529 – 46 * Х;
46 * Х = 64 + 529 – 225;
46 * Х = 368;
Х = 368 : 46;
Х = 8.
ответ: расстояние от дома до места, где рассыпано зерно, составляет 8 м.
Объяснение: