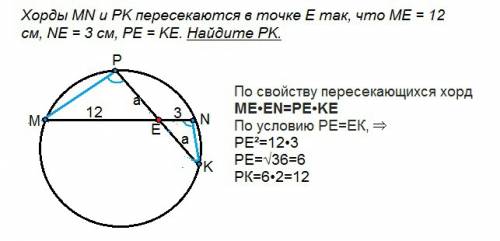
Даны две пересекающиеся хорды. Длины отрезков хорды MN равны 12 и 3. Пусть длины каждого из отрезков второй хорды будут а, т.к. они по условию равны.
Углы с вершинами Р и N вписанные и опираются на одну и ту же дугу. Все вписанные углы, опирающиеся на одну и ту же дугу равны. ⇒ ∠ MPК =∠МNK .
Соединим отрезками точки М и Р и точки K и N
В треугольниках MPЕ и ЕNK углы при Е равны как вертикальные, ∠ MPЕ =∠ЕNK . ⇒
∆ MPЕ ~∆ ЕNK по первому признаку подобия треугольников.
Из подобия следует отношение сходственных сторон:
МЕ:КЕ=РЕ:ЕN ⇒
ME•EN=KE•PE
12•3=а²
а=√36=6
РК=6•2=12 см
________________
Данный решения применён при доказательстве теоремы:
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Её применение сделает запись решения короче:
По свойству пересекающихся хорд
МЕ•EN=PE•KE
По условию РЕ=ЕК, ⇒
РЕ²=12•3
РЕ=√36=6
РК=6•2=12 см
1. 8 см
2. 4√3 см
Объяснение:
1. Сторона А(1)А(2) равна радиусу вписанной окружности, то есть двум диаметрам = 2R
В эту окружность вписан правильный треугольник со стороной 4√3 см.
Радиус окружности, описанной около правильного треугольника со стороной а, равен R = a/√3.
Находим радиус: R = 4√3/√3 = 4 см.
Значит, сторона А(1)А(2) равна 2R = 2*4 = 8 см
2. Сторона А(1)А(2) - это сторона правильного шестиугольника, описанного около окружности, в которую вписан правильный треугольник со стороной 6√3 см.
Сначала находим радиус окружности, описанной около этого правильного треугольника, через его сторону. R = a/√3 = 6√3/√3 = 6 см.
Известно, что правильный шестиугольник разбивается на шесть правильных треугольников с высотой, равной радиусу вписанной окружности. Из этого следует, что сторона правильного шестиугольника находится через радиус вписанной окружности по формуле: а = R/sin 60°.
Находим сторону: а = 6:(√3/2) = 6*2 : √3 = 4√3 см