Задачи такого рода решаются по теореме Пифагора c^2= a^2+b^2 (квадрат гипотенузы равен сумме квадратов катетов). Находим из всех значений наибольшую сторону, в первом случае это корень из 15, следовательно это наша гипотенуза, а корень из 11 и 2 катеты предпологаемого прямоугольного треугольника. Подставив значения в формулу, получаем: 15=11+4. Отсюда следует, что это действительно прямоугольный треугольник. 2) 16=10+6. Тоже прямоугольный. 3) 14=12+2. Прямоугольный. 4) 22=19+8. Не подходит. 5) 17=5+12. Прямоугольный. 6)26=17+9. Прямоугольный. 7) 19=15+4. Прямоугольный.
Назовём данный треугольник АВС.
ВВ1- высота к АС.
АА1=СС1 - высоты к равным боковым сторонам.
Высота равнобедренного треугольника, проведенная к основанию, является его биссектрисой и медианой. ⇒
АВ1=СВ1=30:2=15 см
∆ АВВ1=∆ СВВ1 ( по трем сторонам).
Из ∆ АВВ1 по т.Пифагора
ВВ1=√(AB²-AB1²)=√(17²-15²)=8 см
Высоты к боковым сторонам найдем из площади ∆ АВС
Заметим, что ∆ АВС - тупоугольный ( АС² > АВ²+ВС²), поэтому высоты, проведенные к боковым сторонам тупоугольного треугольника, лежат вне его.
S(ABC)=BB1•AC:2=8•15=120 см²
AA1=2S(ABC):BC
AA1=CC1=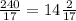 см
см