Определить радиус окружности, определённой уравнением x^2+y^2-4x-6y-3=0.
ответ:Радиус окружности равен 4 условных единицы.
Объяснение:Для начала вспомним общий вид уравнения окружности:
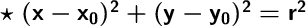
где (x₀;y₀) - координаты центра окружности, r - её радиус.
Мы имеем уравнение окружности. Чтобы найти радиус, нам нужно сделать два полных квадрата в этом уравнении по формулам квадратов разности либо суммы:
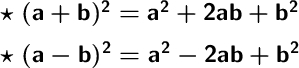
Распишем уравнение окружности по этим формулам:
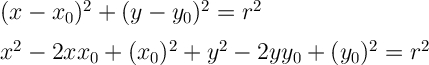
В нашей формуле окружности мы имеем x^2 и y^2, а так же 4x и (-6у). Не сложно догадаться, что (-4х) это и есть то самое (-2хх₀), а (-6у) это (-2уу₀). Отсюда находим координаты середины окружности:
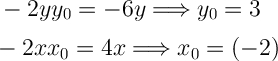
Мы нашли координаты центра нашей окружности - (-2;3).
Теперь нам нужно сделать так, чтобы в нашем уравнении окружности было всё, чтобы сделать там полные квадраты - (х+2)^2 и (y-3)^2.
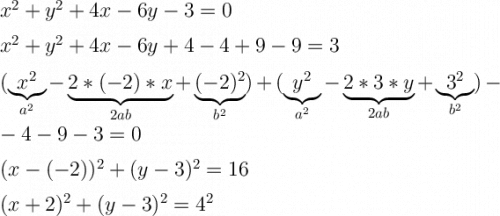
Мы преобразовали наше уравнение окружности. Его центр, как мы уже определили - (-2;3), а радиус - 4.
42.
Объяснение:
Пусть задан треугольник с катетами a и b и гипотенузой c. Высота h = 21 опущена из вершины С на гипотенузу с, а угол А = 60°. Второй острый угол этого прямоугольного треугольника равен
∠В = 90° - 60° = 30°. Больший катет всегда лежит против большего угла, поэтому большим катетом является катет а, лежащий против большего угла А.
Рассмотрим прямоугольный треугольник, образованный большим катетом a заданного треугольника, высотой h, опущенной на гипотенузу и проекцией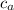 
большего катета a на гипотенузу.
В этом треугольнике гипотенузой является больший катет a заданного треугольника, а высота h = 21 является катетом, лежащим против ∠В = 30° .
Известно, что катет, лежащий против угла в 30°, равен половине гипотенузы. Поэтому b = 2h = 2 · 21 = 42.
1) ∠В=90°-30°=60°
Катет СВ находится напротив угла 30°, значит он равен половине гипотенузы АВ
СВ=1:2=0,5
2)треугольник СНВ - прямоугольный, така как СН-высота,
∠СНВ=90°
3) ∠НСВ=90-60=30°
4) НВ- катет треугольника СНВ, который лежит напротив угла 30° и он равен половине гипотенузы СВ
НВ=0,5:2=0,25
ответ: ВН=0,25.