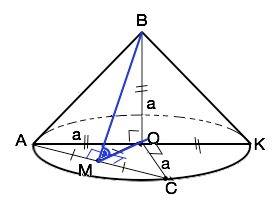
Обозначим данный треугольник АВК, угол В=90°.
Осью симметрии равнобедренного прямоугольного треугольника является высота, проведенная к гипотенузе. В данном случае она же - высота конуса и равна радиусу его основания, так как является еще медианой. ( свойство),
Центральный угол АОС равен дуге, на которую опирается, т.е. 90°.
Хорда АС является основанием равнобедренного прямоугольного треугольника АОС с катетами, равными радиусу конуса.
Плоскость АВС и плоскость основания конуса образуют двугранный угол, который измеряется величиной его линейного угла.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.
Проведем высоту ОМ ( она же медиана) ∆ АОС.
ОМ⊥АС. По т. о 3-х перпендикулярах наклонная ВМ⊥АС.
Угол ВМО - искомый.
Примем радиус и высоту конуса равными а. Высота ВО конуса перпендикулярна основанию, следовательно, перпендикулярна любой прямой, проходящей в плоскости основания через О .
∆ ВОМ - прямоугольный.
В ∆ АОС медиана ОМ равна АМ, т.е. половине АС ( свойство медианы).⇒
∆ АОМ равнобедренный прямоугольный, его острые углы равны 45°
ОМ=ОА•sin45°=a•√2/2.
tg∠ВМО=ВО:МО=(а:(а√2:2)=√2
Если требуется выразить его в градусах, угол ВМО=54°44'
1. Так как периметр равнобедренного треугольника равен 36 значит 36:3=12. Так как AC основания значит P=ADC=12+AD+AC. Значит 36-12=24 и 24:2=12
2. ответ 2
3. ответ 1
4. Если биссектриса является высотой, то треугольник
ABC равнобедренный. АВ=Вс. Периметр Авд
равен периметру ВСД и равен 14 см. Чтобы узнать
периметр ABC надо из суммы двух периметров
маленьких треугольников вычесть двойную
высоту, т.к. она присутствует и в периметре
АВД и в периметре ВДС. Итого периметр ABC =
14 +14-3-3=22 см.
5. Угол 1 и угол 3 - вертикальные,значит они равны
угол 1 и угол 3= 178:2=89
угол 2 и угол 3 - смежные,значит их сумма равна
180
угол 23 180-угол 3,
угол 2 =180- 89=91
угол 4 и угол 2- вертикальные,значит они равны
угол 2 = углу 4 = 91