9. равнобедренном треугольнике с периметром 50 см боковая сторона относится к основанию как 3: 4. найдите стороны треугольника. рисунок: решение:

👇

Ответ:

Banan125027

11.11.2020

Дано:АВС
Р=50см
АВ:АС=3:4
АВ, АС, ВС- ?

1) пусть коэффициент пропорциональности тогда АВ=3x а АС=4х
по свойству равнобедренного треугольника АВ=ВС=3х
Зная что Р=50см составляем уравнение:
3х+3х+4х=50
10х=50
х=50:10
х=5
таким образом АВ=15см, ВС= 15см, АС=20

4,7(24 оценок)

Открыть все ответы

Ответ:

nastakianka

11.11.2020

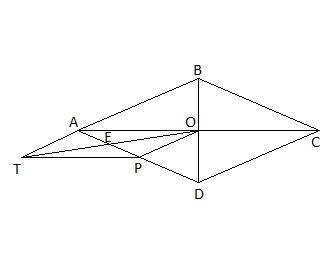
Т.к. диагональ AP параллелограмма AOPT разбивает его на два равных треугольника, то

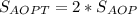
$S_{AOPT}=2*S_{AOP}$

Т.к. OP - медиана в ΔAOD, то она разбивает его на два равновеликих треугольника ⇒

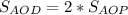
$S_{AOD}=2*S_{AOP}$

Отсюда:

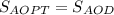
$S_{AOPT}=S_{AOD}$

Площадь прямоугольного треугольника найдем как полупроизведение катетов, которые являются половинами диагоналей ромба (точка O делит диагонали ромба пополам:

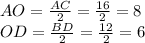
$AO=\frac{AC}{2}=\frac{16}{2}=8\\OD=\frac{BD}{2}=\frac{12}{2}=6$

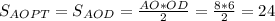
$S_{AOPT}=S_{AOD}=\frac{AO*OD}{2}=\frac{8*6}{2}=24$

Из прямоугольного ΔAOD найдем его гипотенузу:

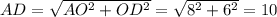
$AD=\sqrt{AO^2+OD^2}=\sqrt{8^2+6^2}=10$

Т.к P - середина стороны AD, то AP = AD / 2 = 10 / 2 = 5

Для параллелограмма сумма квадратов диагоналей равна сумме квадратов его сторон:

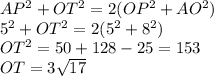
$AP^2+OT^2=2(OP^2+AO^2)\\5^2+OT^2=2(5^2+8^2)\\OT^2=50+128-25=153\\OT=3\sqrt{17}$

Площадь параллелограмма равна также полупроизвведению диагоналей на синус угла между ними:

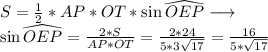
$S=\frac{1}{2}*AP*OT*\sin{\widehat{OEP}}\longrightarrow\\\sin{\widehat{OEP}}=\frac{2*S}{AP*OT}=\frac{2*24}{5*3\sqrt{17}}=\frac{16}{5*\sqrt{17}}$

По основному тригонометрическому тождеству найдем косинус угла между диагоналями по известному синуса угла:

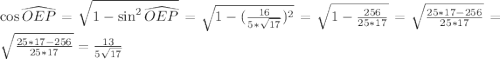
$\cos{\widehat{OEP}}=\sqrt{1-\sin^2{\widehat{OEP}}}=\sqrt{1-(\frac{16}{5*\sqrt{17}})^2}=\sqrt{1-\frac{256}{25*17}}=\sqrt{\frac{25*17-256}{25*17}}=\sqrt{\frac{25*17-256}{25*17}}=\frac{13}{5\sqrt{17}}$

Диагонали ромба abcd пересекаются в точке o. отрезок op - медиана треугольника aod. на отрезках ao и

4,6(36 оценок)

Ответ:

khorolovgusenoy2lzx

11.11.2020

Расстояние от точки до прямой ---на перпендикуляре из точки к этой прямой)))
нужно построить прямую из В перпендикулярно к А1D1
A1D1 _|_ AA1 т.к. призма правильная (т.е. прямая)
AD --проекция A1D1 на основание
но A1D1 НЕ перпендикулярно В1А1 (как и AD не перпендикулярно АВ)))
построим ВТ _|_ AD
B1T1 _|_ A1D1
плоскость (ТВВ1) перпендикулярна плоскости (AA1D1)
BT1 _|_ A1D1
треугольник ВТТ1 --прямоугольный, ВТ1 --гипотенуза)))
искомое расстояние BT1 = √(BT² + TT1²) = √((3/4) + 1) = √7 / 2
BT --высота равностороннего треугольника = а√3/2
((в правильном 6-угольнике сторона 6-угольника = радиусу описанной окружности)))
C2 в правильной шестиугольной призме , все ребра которой равны 1, найдите расстояние от точки в до п