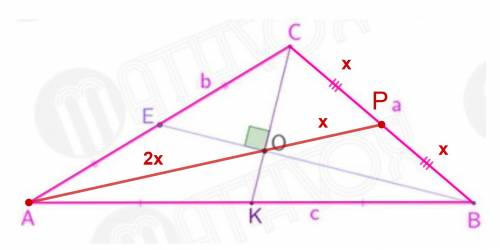
1) Проведем медиану AP, ⇒ CP = PB.
2) AO:OP = 2:1 (по свойству пересекаемых медиан)
3) ΔCOB — прямоугольный, т.к. CO⊥BO (CO∈CK, BO∈BE, CK⊥BE по условия задачи)
4) OP — медиана ΔCOB, т.к. ΔCOB — прямоугольный, CP = PB, а медиана делит сторону, на которую опущена, только в прямоугольном треугольнике, и эта сторона — гипотенуза, а угол, с которого проведена медиана — прямой.
Следовательно, OP = 1/2CB, или OP:CB = 1:2
5) AP:CB = (AO+OP):CB = (2+1):2 = 3:2.
ответ: отношение третьей медианы к соответствующий стороне — 3:2.
По условию, FBDE - ромб ⇒ FB = BD = DE = FE и ∠DBE = ∠BFE.
Пусть , BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
, BE - высота треугольника ABC и биссектриса острых углов ромба FBDE , то ΔABC - равнобедренный ⇒ ∠BAC = ∠BCA = α.
Отрезок АС виден под прямыми углами, следовательно, точки A, F, D, C лежат на окружности ⇒ DE - медиана и радиус окружности, следовательно, DE = EC ⇒ ΔDEC - равнобедренный ⇒
∠EDC = ∠DCE = α. Тогда ∠DBE = 180° - α. Известно, что сумма углов четырехугольника равна 360°.
2∠FBD + 2∠DBE = 360°
2∠FBD + 360° - 2α = 360°
∠FBD = α
Таким образом, ∠A = ∠B = ∠C ⇒ ΔABC - равносторонний.