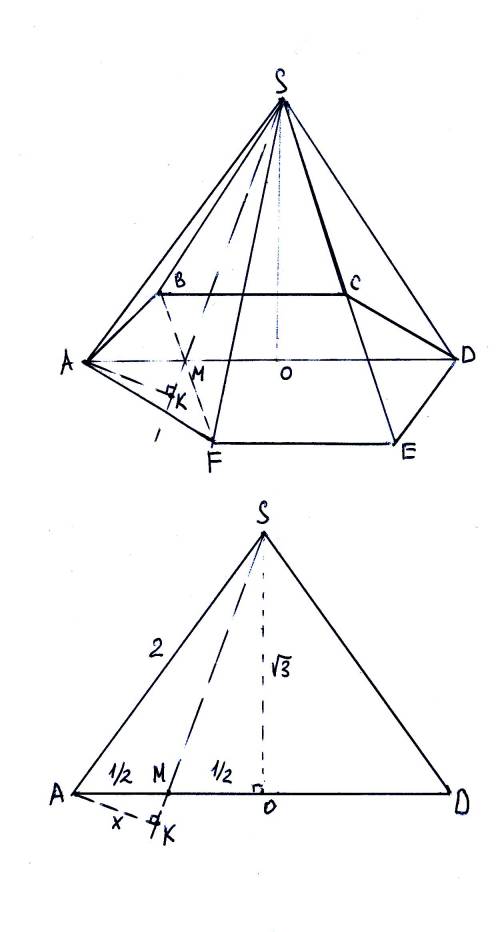
см. чертеж, верхний рисунок.
Я не буду тратить время на объяснение простых вещей - постарайтесь обосновать их самостоятельно, это очень просто.
BF перпендикулярно AD (обоснуйте), SO перпендикулярно основанию, а - значит - и BF. Поэтому => BF перпендикулярно плоскости ASD (то есть всем прямым в этой плоскости).
Если в плоскости ASD провести перпендикуляр АК к продолжению SM (М - середина BF), то АК и есть расстояние от А до SBF, поскольку АК перпендикулярно BF и SM, то есть всей плоскости SBF.
см. чертеж, нижний рисунок.
Это - плоскость ASD. В ней AD = 2 (обоснуйте), поэтому треугольник ASD - равносторонний (все стороны равны 2).
Треугольники АМК и SMO подобны (прямоугольные с равными острыми углами), поэтому АК/AM = SO/SM;
AK = x; AM = MO = 1/2;
SM^2 = 3 + (1/2)^2 = 13/4; SM = √13/2;
2*x =2*√3/√13; x = √(3/13);
определить каноническое уравнение гиперболы, если угол между асимптотами равен 60 градусов и С= 2 корня из 3.
Угол между асимптотой и осью Ох равен 60/2 = 30 градусов.
Угловой её коэффициент или тангенс угла наклона к оси Ох равен
1/√3. Значит, в уравнениях асимптот у = +-(b/a)x значение b/a = 1/√3.
Отсюда находим соотношение a = b√3.
Далее используем заданное значение с = 2√3.
Так как с² = a² + b², то используем найденное соотношение a и b .
(2√3)² = (b√3)² + b²,
12 = 3b² + b²,
12 = 4b²,
b² = 12/4 = 3,
b = √3.
Тогда а = b√3 = √3*√3 = 3.
Найдены параметры a и b канонического уравнения параболы:
(x²/a²) - (y²/b²) = 1.
Подставляем найденные параметры и получаем
ответ: (x²/3²) - (y²/(√3)²) = 1.
Эксцентриситет гиперболы равен е = с/а = 2√3/3.
Уравнения асимптот у = +-(√3/3)x.
Координаты фокусов F1,F2 = (+-2√3; 0).
Уравнения директрис х = +-a²/c = +-3√3/2.