Пусть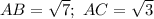 
. Из условия AE = BC, а так как
AM - медиана треугольника ABC, то BE = EC = BC/2 = AE/2.
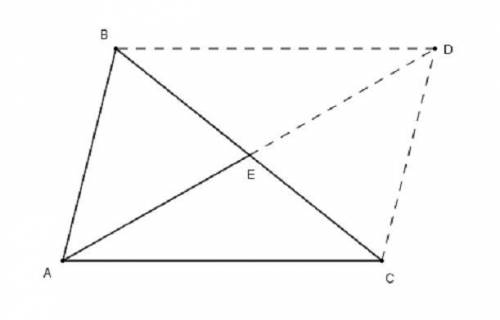
Сделаем дополнительное построение, т.е. построим до параллелограмма ABDC, в нём AD = 2AE = 2BC, тогда сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
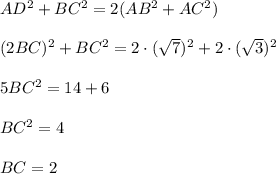
Не трудно заметить, что треугольник ABC - прямоугольный с гипотенузой AB = √7 и катетами AC = √3; BC = 2.
2) Площадь треугольника: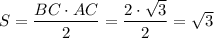 
кв. ед.
3) Центр описанной окружности лежит на середине гипотенузы, значит радиус описанной окружности равен половине гипотенузы.
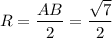
В прямоугольном треугольнике гипотенуза — самая большая сторона.
По т. Пифагора (гипотенуза)²= (катет1)²+(катет2)².
а) 12, 9, 15. Сторона 15 - гипотенуза.
15²=12²+9²;
225=144+81;
225=225 => треугольник является прямоугольным.
б) 13, 14, 15. Сторона 15 - гипотенуза.
15²=14²+13²;
225=196+169;
225 ≠ 365 => треугольник не прямоугольный.
в) 2, 5, 4. Сторона 5 - гипотенуза.
5²=4²+2²;
25=16+4;
25 ≠ 20 => треугольник не прямоугольный.