ответ во вложении Объяснение:
Пусть A' – середина дуги BC. Так как OA' || IA2, прямые OI и A'A2 пересекаются в точке K – центре гомотетии описанной и вписанной окружностей (см. рис.). Докажем, что K – искомый радикальный центр.
Первый Так как инверсия с центром A' и радиусом A'B меняет местами прямую BC и описанную окружность Ω треугольника ABC, точка A1 переходит в A, а A2 – в точку A'' пересечения прямой A'A2 с описанной окружностью. Следовательно, точки A, A1, A2 и A'' лежат на одной окружности.
Степень точки K относительно описанной окружности треугольника AA1A2 равна – KA2·KA'' = – r/R AA'·KA'' = r/R s(K), где s(K) – степень точки K относительно Ω.
Очевидно, степени точки K относительно описанных окружностей треугольников BB1B2 и CC1C2 будут такими же, то есть K – радикальный центр трёх окружностей.
Второй Пусть A', B', C' – середины дуг BC, CA, AB. Тогда треугольник A'B'C' переводится в A2B2C2 гомотетией с коэффициентом r/R и центром K, то есть KA2 : A'A2 = KB2 : B'B2 = KC2 : C'C2 = k : 1. Для точек прямой A'A2 разность степеней относительно описанной окружности треугольника AA1A2 и вписанной окружности треугольника ABC является линейной функцией. В точке A2 эта функция равна нулю,
а в точке A' – r², поскольку A'A1·A'A = A'B² = A'I² (первое равенсто следует из подобия треугольников A'A1B и A'BA, а второе – из леммы о трезубце – см. задачу 53119). Значит, в точке K эта разность равна – kr². Другие аналогичные разности в точке K также равны – kr², откуда и следует требуемое
Объяснение:
Я не очень умею объяснять, но попробую
Крч провели мы эти линии и получили несколько паралеллогрмаммов (я наверное ушла не в ту степь, но пофиг), а у них противоположные стороны равны. Так мы нашли отрезки В1В, ВА1, А1С, СС1, С1А, АВ1. Мы видим, что каждая прямая состоит из двух одинаковых отрезков, равных одной из сторон исходного треугольника, значит каждая сторона ⚠︎С1В1А1 в два раза больше параллельно лежащей стороны ⚠︎АВС, следовательно периметр С1В1А1 будет в два раза больше, чем у АВС
На фото можно увидеть решение( "дано" не будет оно приняло ислам)


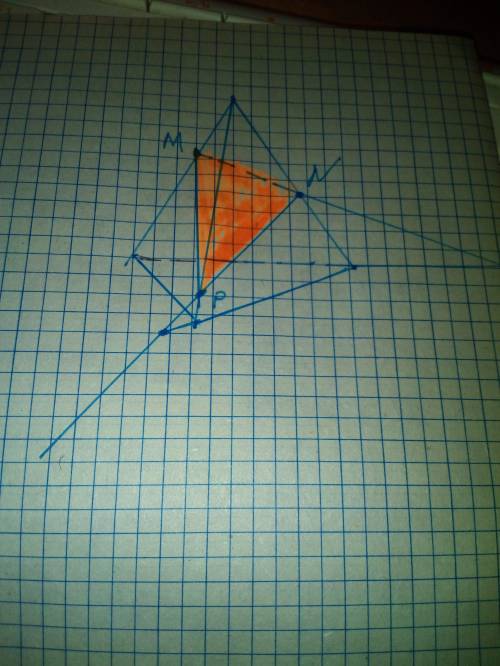
искомое сечение MNP
Объяснение:
построение
1. MN, точки M и N принадлежат одной грани ( плоскости)
2. NP
3. MP
4. ∆ MNP - искомое сечение, заштриховать