Основой пирамиды кавсd является квадрат авсd со стороной 10 см. грани кав и ксо перпендикулярны плоскости основания, а две другие грани образуют угол 45° с плоскостью основы. установите соответствие между величинами (1 - 4) и их числовыми значениями (а - е).
1 высота пирамиды
2 длина ребра кd
3 площадь боковой поверхности пирамиды
4 сумма площадей диагональных сечений
а 10
б 10√2
в 10√3
г 50 (√2 + √3)
д 100 (1 + √2)
е 100 (2 + √2)
(основою піраміди кавсd є квадрат авсd зі стороною 10 см. грані кав та ксв
перпендикулярні до площини основи, а дві інші грані утворюють кут 45о
із площиною основи. установіть відповідність між величинами ( 1 – 4 ) та їх числовими значеннями (а – е).
1 висота піраміди
2 довжина ребра кd
3 площа бічної поверхні піраміди
4 сума площ діагональних перерізів
а 10
б 10√2
в 10√3
г 50(√2 + √3)
д 100(1 + √2)
е 100(2 +√2))
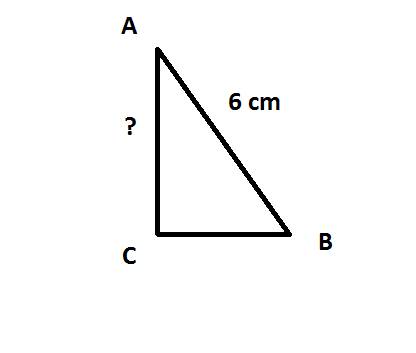
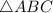 . Из условия ясно, что он — прямоугольный (так как
. Из условия ясно, что он — прямоугольный (так как 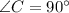 ).
). 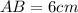 — гипотенуза,
— гипотенуза, 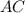 — искомый катет,
— искомый катет, 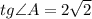
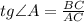
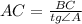
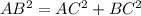
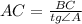 .
.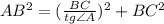
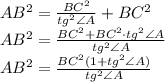
 :
: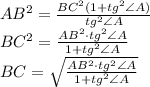
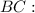
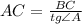
 новую подстановку:
новую подстановку: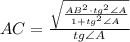
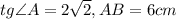
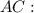
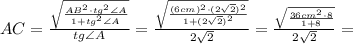
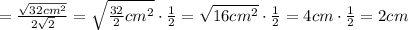

.......................................