Дано : ΔABC остроугольный
AK ⊥ BC ; BD ⊥ AC ; AH =BC , H = AK ∩ BD ( H - точка пересечения высот)
∠BAC -?
ответ: 45° .
Объяснение:
Прямоугольные треугольники HDA и CDB равны ( третий признак равенства _ по гипотенузе и острому углу )
ΔHDA = ΔCDB
* * * ∠HDA = ∠BDC = 90 ° * * *
AH = BC ( гипотенузы по условию )
∠AHD =∠BCD углы со взаимно перпендикулярными сторонами : AH⊥ BC ; HD ⊥ AC (снова по условию) ,
следовательно AD = BD , т.е. прямоугольный треугольник ΔADB равнобедренный ⇒∠BAC = ∠ABC = 45° .
( ! Равенство второго пара катетов: HD = CD можно использовать при построения правильного чертежа. )
* * * Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника, то такие прямоугольные треугольники равны ( аналог второго признака равенства для "обычных "треугольников" ) * * *
* * * AK ⊥ BC ⇔ AH⊥ BC ; BD ⊥ AC ⇔ HD ⊥ AC ))) * * *
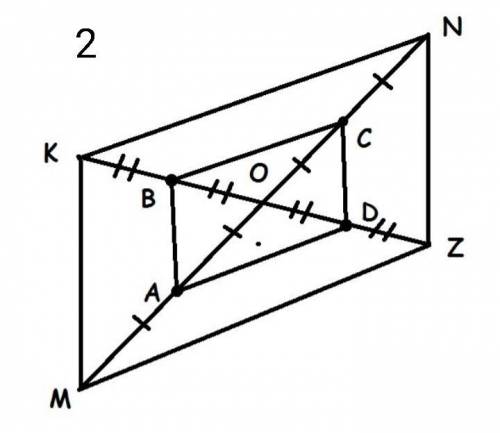
2.Рассмотрим параллелограмм MKNZ.
MO = ON, KO = OZ т.к. диагонали параллелограмма в точке пересечения делятся пополам
MA = AO, OC = CN по условию.
AO = MO : 2, OC = ON : 2 По условию.
MO = ON Из этого следует, что AO = OC
KB = BO, OD = DZ по условию.
BO = KO : 2, OC = OZ : 2 По KO = OZ Из этого следует, что BO = OD
Рассмотрим четырёхугольник ABCD
Диагональ BD в точке О делит диагональ AC на 2 равных отреДиагональ AC в точке О делит диагональ BD на 2 равных отрезка
ответ: Четырёхугольник ABCD является параллелограммом т.к. его диагонали делятся пополам в очке пересечения
3.Решение:
Средняя линия треугольника равна половине основания треугольника, следовательно основание треугольника равно: 7*2=14 (м) , т.к. меньшее основание образовавшейся трапеции, есть средняя линия треугольника, равная 7м
Зная что средняя линия треугольника делит боковые стороны трегольника пополам, боковые стороны треугольники равны:
- первая 5*2=10(м)
-вторая 6*2=12(м)
Отсюда:
периметр треугольника равен: 14+10+12=36(м)
ответ: Р=36м
4......
Это естественно не мой ответы :)


Задача первая.
Дано: треугольник KTM - равнобедренный.
KM - основание,
угол1 = 50°,
угол2 = 100°.
Найти: углы.
Решение: обозначим угол TKM как угол3, тогда угол1 и угол3 - вертикальные, значит угол1 = углу3 = 50°.
обозначим угол KTM как угол4, тогда угол2 и угол4 - смежные, значит угол4 = 180° - угол2 = 180° - 100° = 80°.
если угол3 = 50° и угол4 = 80°, то угол M = 180° - 50° - 80° = 50°
ответ: ∠TKM = 50°, ∠M = 50° и ∠KTM = 80°.
Задача вторая.
Дано: PMK - треугольник.
PK = PM,
PH - медиана,
∠MPK = 42°.
Найти: ∠PHK и ∠KPH.
Решение: т.к. PK = PM, то треугольник KPM - равнобедренный, значит PH - медиана биссектриса и высота (по свойству равнобедренного треугольника). если PH - высота, то угол PHK = 90°.
если угол MPK = 42°, а PH - биссектриса, то угол KPH = угол MPK : 2 = 42° : 2 = 21°.
ответ: 90° и 21°.
Удачи!!