

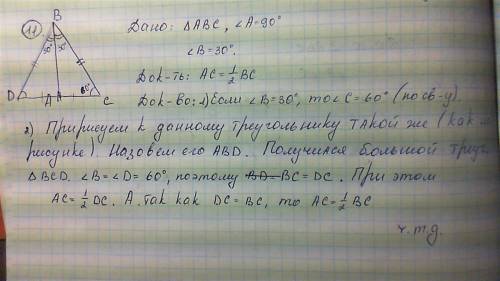
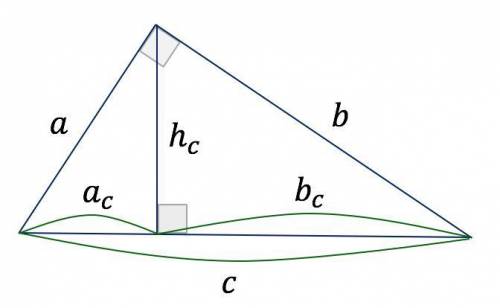
Для даної задачі треба скористатися властивостями катетів та їх проекцій на гіпотенузу в прямокутному трикутнику.
Перший б
Катет прямокутного трикутника — середнє пропорційне між гіпотенузою  і проекцією цього катета на гіпотенузу:
і проекцією цього катета на гіпотенузу:
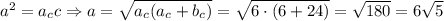 см
см
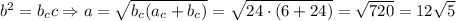 см
см
Площа  прямокутного трикутника знаходится як півдобуток його катетів:
прямокутного трикутника знаходится як півдобуток його катетів:
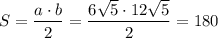 см²
см²
Другий б
Висота 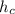 прямокутного трикутника, що проведена до гіпотенузи
прямокутного трикутника, що проведена до гіпотенузи  з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
з вершини прямого кута, — середнє пропорційне між проекціями катетів на гіпотенузу:
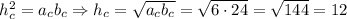 см
см
Площа 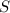 будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи
будь-якого трикутника знаходиться як півдобуток його сторони на висоту, що проведена до цієї сторони. У нашому випадку — це півдобуток гіпотенузи  і висоти
і висоти 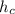 , що до неї проведена:
, що до неї проведена:
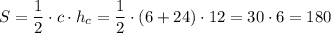 см²
см²
Відповідь: 180 см².
Опустить перпендикуляры на МД и МА из центра (пусть N и S соответственно) Рассмотреть прямоугольник ОSMN . Искомая МО - диагональ нашего четырехугольника. МS =(15+6) = 21=NO; Далье рассмотрим треугольник NOD (ОD - радиус окружности =R; ND = 1/2(CD)=2V46; ) NO=21 из прямоугольника ; Найдем радиус по теореме пифагора( R)2 = (NO)2+(ND)2 (2 - это в квадрате);Радиус равен 25. Из треугольника АSO (AO =R=21; AS = 15(как половина АВ) найдем SO по теореме пифагора. SO =V (625-225) = 20; SO=MN =20; Теперь из треугольника ОSM найдем МО по теореме Пифагора. OM= V(20^2+21^2) = V841 = 29