ОДЗ: Sinx≠0
0≤Cosx≤1
x∈[π/2+πk, 2πk) k∈Z
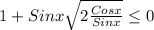
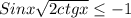
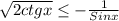
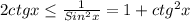
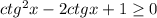
(ctgx-1)² ≥ 0
ctgx=1
ответ: x=-3π/4+2πk, k∈Z
а) b = 18 б) b = 10 в) y=20 г) y = 1,2
д) a = 9 е) a = 24 ж) x = 1,4 з) x = 0,6
Объяснение:
Основное свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции.
a : b = c : d ⇒ ad = bc
а) 2 : 9 = 4 : b; 2b = 9*4; 2b = 36; b = 36 : 2; b = 18;
б) 15 : b = 3 : 2; 15*2 = b*3; 30 = 3b; b = 30 : 3; b = 10;
в) 3 : 2,1 = y : 14; 3 * 14 = 2,1y; 42 = 2,1y; y = 42 : 2,1; y = 20;
г) y : 2,4 = 3 : 6; 6y = 2,4*3; 6y = 7,2; y = 7,2 :6; y = 1,2;
д) 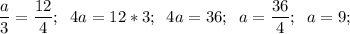
е) 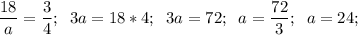
ж) 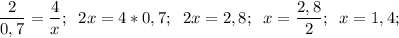
з) 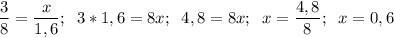
В правой части уравнения степень "2 * (x² - 15)" расписываем:
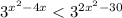
Степени одинаковые и больше единицы, их опускаем без изменения знака:
x² - 4x < 2x² - 30
x² + 4x - 30 > 0
Решаем квадратное уравнение:
D = b² - 4ac = 16 - 4 * (-30) = 136
Выделим целую часть из корня:
√136 = √2² * √34 = 2√34
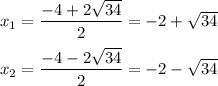
Степени все нечётные (равны 1 в данном случае), минуса никакого перед скобками нет, значит, справа ставим знак "+", а потом чередуем знаки.
(x + 2-√34)(x+2+√34) > 0
Нас волнует только положительные значения, поэтому выбираем промежутки с плюсом.
ответ: x ∈ (-∞; -2-√34) ∪ (-2+√34; +∞)
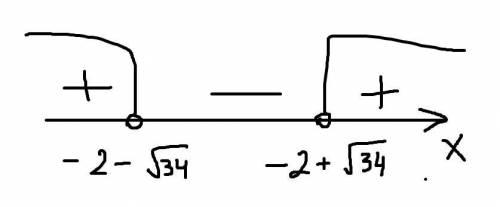
1+sinx·√(2ctgx) ≤ 0
Подкоренное выражение не может быть отрицательным
ctg x ≥ 0 0.5π ≥ x > 0 это в 1-й четверти
1.5π ≥ x > π это в 3-й четверти
в 1-й четверти sinx > 0 и выражение 1+sinx·√(2ctgx)> 0
в 3-й четверти sinx < 0 и выражение 1+sinx·√(2ctgx)может стать меньше 0, если
sinx·√(2ctgx) ≤ -1
делим на отрицательный синус
√(2ctgx) ≥ -1/sinx
обе части положительны
возводим в квадрат
2ctgx ≥ 1/sin²x
2ctgx ≥ 1 + ctg²x
1 + ctg²x - 2ctgx ≤ 0
(1 - ctgx)² ≤ 0
Квадрат любого числа не может быть отрицательным, поэтому остаётся только
равенство нулю:
1 - ctgx = 0
ctgx = 1 (четверть 3-я!)
х = 5/4π
Решение единственное: при х = 5/4π выражение 1+sinx·√(2ctgx) = 0
ну, и, разумеется следует добавить 2πn, тогда решение такое:
х = 5/4π +2πn