Объяснение:
Площадь по векторам:
Найдем векторы по координатам точек:
AB = {Bx - Ax; By - Ay; Bz - Az} = {-1 - (-4); 5 - (-1); -1 - 4} = {3; 6; -5}
AC = {Cx - Ax; Cy - Ay; Cz - Az} = {3 - (-4); 3 - (-1); -1 - 4} = {7; 4; -5}
S= (1 /2) |AB × AC|
Найдем векторное произведение векторов:
c = AB × AC
AB × AC =
i j k
ABx ABy ABz
ACx ACy ACz
=
i j k
3 6 -5
7 4 -5
=
= i (6·(-5) - (-5)·4) - j (3·(-5) - (-5)·7) + k (3·4 - 6·7) = i (-30 + 20) - j (-15 + -35) + k (12 - 42) = = {-10; -20; -30}
Найдем длину (модуль) вектора:
|c| = √(cx2 + cy2 + cz2) = √((-10)2 + (-20)2 + (-30)2) =
= √(100 + 400 + 900) = 1400 = 10·√14
Найдем площадь треугольника:
S = (1 /2) · 10·√14 = 5·√14 ≈ 18.708287.
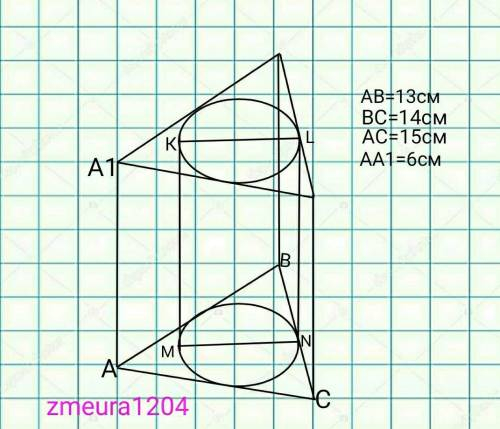
1) пів-периметр призми дорівнює 21см
2) площа основи призми дорівнює 84см²
3) радіус циліндра дорівнює 4см
4) площа осьового перерізу циліндру дорівнює 48см²
5) діагональ осьового перерізу циліндра дорівнює 10см
6) площа повної поверхні призми дорівнює 420см²
7) Площа поверхні циліндра дорівнює 80π см²
8) Об'єм циліндра дорівнює 96π см³
9) Об'єм призми дорівнює 504 см³
Объяснение:
1)
р=(АВ+ВС+АС)/2=(13+14+15)/2=
=42/2=21см
2)
S(∆АВС)=√(p(p-AB)(p-BC)(p-AC))=
=√(21(21-13)(21-14)(21-15))=
=√(21*8*7*6)=√(7*3*4*2*7*2*3)=
=7*3*4=84см²
3)
r=S(∆ABC)/p=84/21=4см
4)
МК=АА1=6см
MN=2r=2*4=8см
S(MKLN)=MK*MN=6*8=48см²
5)
∆МКN- прямокутний трикутник.
Теорема Піфагора:
КN=√(MK²+MN²)=√(6²+8²)=
=10см
6)
Р(∆АВС)=2*р=2*21=42см
Sб=Р(∆АВС)*АА1=42*6=252см²
Sп.п.=Sб+2*S(∆ABC)=
=252+2*84=252+168=420см²
7)
Sо.ц.=πr²=4²π=16π см²
Sб.ц.=S(MKLN)*π=48π см²
Sп.ц.=Sб.ц.+2*Sо.ц=
=48π+2*16π=48π+32π=80π см²
8)
Vц=Sо.ц.*МК=16π*6=96π см³
9)
Vпр.=S(∆ABC)*AA1=84*6=504см³
Решение во вложении.