1. Вспомним признак прямоугольника: если в четырёхугольнике три угла равны по 90°, то этот четырёхугольник - прямоугольник. Рассмотрим и проверим этот признак в данной задаче:
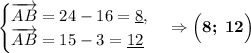
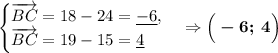
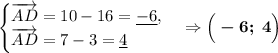
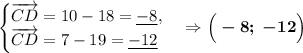
Вспомним свойство о скалярном произведении векторов: если произведение двух ненулевых векторов равно нулю, то эти векторы перпендикулярны. Найдём такие пары векторов:
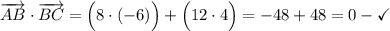
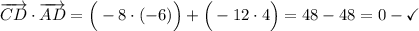
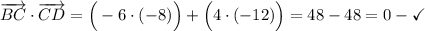
Теперь мы можем утверждать, что фигура "ABCD" - прямоугольник, т.к. углы "B", "C" и "D" составляют по 90° каждый.
Что и требовалось доказать.
2. Площадь прямоугольника - произведение его длины и ширины. Поэтому сначала нужно найти, чему равна длина и ширина.
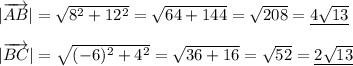
Теперь, когда нам известна и длина, и ширина, найдём площадь прямоугольника:
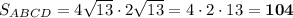 см².
см².
ответ: 104 см².
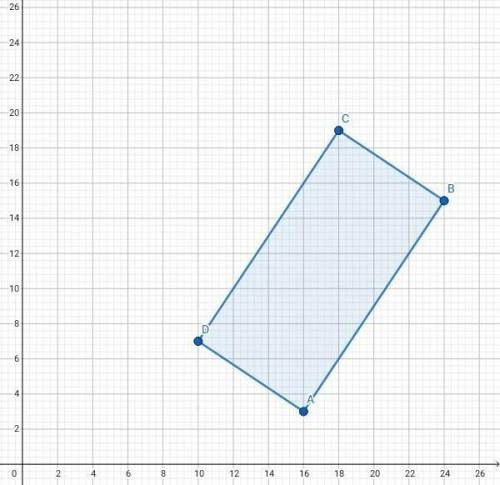
ABCD - прямоугольник, АС - диагональ. Пусть ∠BCA = 60°.
∠BAC = 90° - 60° = 30°; BC = 0.5AC = 9 см (против угла 30° катет в два раза меньше гипотенузы). По т. Пифагора AB² = 18² - 9² = 9√3 см
S = 9√3 · 9 = 81√3 см²