Сторона правильного шестиугольника равна радиусу описанной окружности, т.е. а = R.
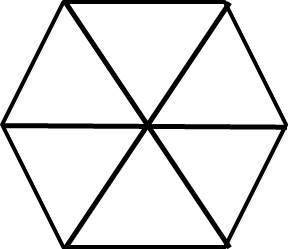
Т.к. проведя все радиусы в шестиугольнике, вписанном в окружность, мы разобьем его на 6 равносторонних треугольников (см. рис.), а площадь получившегося треугольника можно найти по формуле
1/2 · R · R · sin60° = 1/2 · R² · √3/2 = R²√3/4
(полный круг составляет 360°, тогда угол при вершине равностороннего треугольника будет равен 60°, а sin60° = √3/2), то площадь шестиугольника будет равна:
6 · R²√3/4 = 3R²√3/2 = 3 · 2²√3/2 = 6√3 (см²)
ответ: 6√3 см².
ответ: 123 см
Объяснение: ∠В=∠Д=150° , ∠АВК=150°-90°=60°. В ΔАВК ∠К=90° т.к. ВЛ ⊥АД по условию, ∠А=90°-60°=30° , ВК=АВ:2=18:2=9 (см), ВС=1,5 * АВ= 1,5 * 18=27 (см)
Площадь параллелогр. S= BC * BK=27*9=123 (см²) ответ: 123 см²