Объяснение:
1. находим боковые стороны равнобедренного треугольника через его площадь:
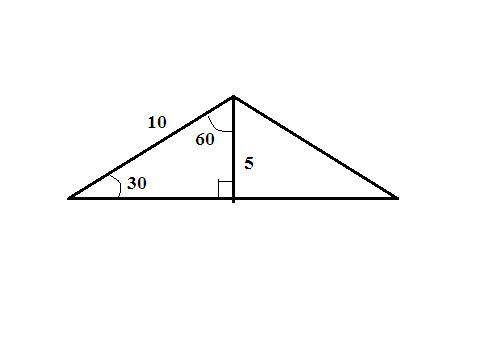
S=a²sin120°/2 ⇒ a²=(25√3)/(√3/2)/2=25*4, a=√(25*4)=5*2=10 см - боковые стороны.
2. находим основание:
высота, проведенная к основанию равнобедренного треугольника, образует с боковой стороной и половиной основания прямоугольный треугольник где гипотенуза - боковая сторона - 10 см. Углы в этом треугольнике 90°, 60°, 30°. Против угла 30° (высота треугольника) лежит катет в два раза меньше гипотенузы ⇒ высота - 10/2=5 см;
далее либо по т. Пифагора находим половину основания треугольника, либо через формулу нахождения площади находим длину всего основания.
т. Пифагора: √(10²-5²)=√75=5√3 см - половина основания, (5√3)*2=10√3 - основание треугольника;
через площадь: в*h/2=25√3, в=50√3/5=10√3 см.
Можно решить
Из прямоуг. треуг-ка АОВ найдем катеты( равны радиусу) 2Rквад = 324, или Rквад = 162. Теперь по известной формуле для прямоуг. тр-ка найдем искомое расстояние, а именно - высоту, опущенную на гипотенузу:
h = Rквад/АВ = 9см
треугольник АОВ - равнобедренный и прямоугольный по теореме Пифагора ОА = ОВ = 18 : sqrt2 = 9*sqrt2 обозначим h - расстояние от точки О до хорды, этот отрезок будет перпендикулярен хорде тогда площадь треугольника АОВ = ОА*ОВ/2 = АВ*h/2 отсюда h = ОА*ОВ/АВ = (9*SQRT2)^2/18 = 9 см