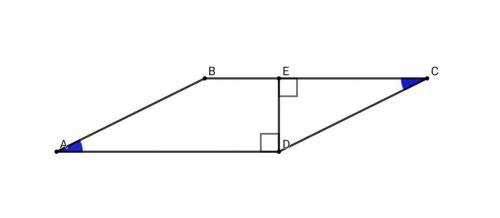
В четырёхугольнике ABCD по условию противолежащие стороны попарно равны ⇒ ABCD - параллелограмм
Противолежащие углы параллелограмма попарно равныУглы, прилежащие к любой стороне параллелограмма, в сумме равны 180°∠А + ∠В = 180°, ∠В = 180° - ∠A = 180° - 30° = 150° ⇒ ∠B = ∠D = 150°
∠ADE = ∠D - ∠CDE = 150° - 60° = 90°
Прямоугольная трапеция - это трапеция, боковая сторона которого перпендикулярна основаниямВЕ || AD, AB∦(не параллельно) ED, DE⊥BE, DE⊥AD ⇒ ABED - прямоугольная трапеция, что и требовалось доказать.
Да, может, т.к. сумма двух других должна быть меньше 180°, и это возможно только при условии : при основании быть тупого или прямого угла не может, т.к. они равны и в сумме составят больше 180° или 180°. Но если при основании сумма меньше 180°, то при вершине может быть любой угол, как острый, так или тупой или прямой.
ответ может.