Объяснение: ЗАДАНИЕ 1
Сумма угло ромба и любого четырёхугольника составляет 360°. У ромба противоположные углы между собой равны, поэтому легко можно найти каждый угол:
360-226=134°
Нам известны попарно суммы углов, теперь найдём каждый из них:
226÷2=113°
134÷2=67°
ответ: острый угол ромба =67°
ЗАДАНИЕ 2
Найдём площадь пола:
Sпол=12,5×5,4=67,5м²
Переведём площадь в сантиметры:
67,5×100=6750см²
Теперь найдём площадь дощечки:
S=25×10=250см²
Теперь поделим эти площади друг на друга: 6750÷250=27дощ
ответ: 27дощ.
ЗАДАНИЕ 3
Найдём гипотенузу по теореме Пифагора: квадрат гипотенузы равен сумме квадратов катетов:
Гипот=√(16²+30²)=√(256+900)=
=√1156=34см
Итак гипотенуза=34см
Так как медиана проведена к гипотенузе, то она проведена из прямого угла, поэтому медиана равна половине гипотенузы: 34÷2=17см
ответ: медиана=17см
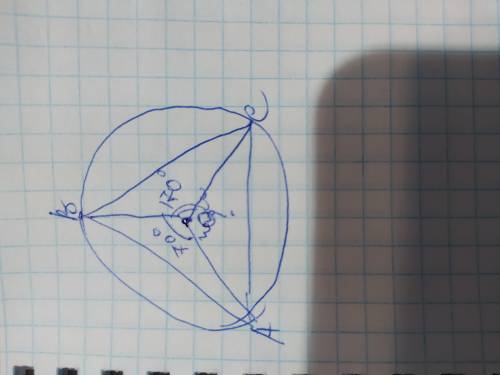
ЗАДАНИЕ 4
Сумма всех углов окружности составляет 360°, и так как нам известны 2 из них, найдём искомый:
Угол дуги АС=360-70-170=120°
ОТВЕТ: угол дуги АС=120°
S=68см²
Объяснение:
якщо скласти ці відрізки, то уся сторона буде 15+2=17см. Нам відомо, що трикутник рівнобедрений, тоді друга сторона теж=17см. Трикутник, з висотою є прямокутним і відомо в ньому 2 сторони: катет=15см і бічна сторона, яка є гіпотенузою. За теоремою Піфагора, знайдемо висоту: h=√(17²-15²)=√(289-225)=√64=8см
висота h=8см. Якщо відома висота, знайдемо площу трикутника. Площа трикутника дорівнює ½ добутку її сторони і висоти проведенoї до неї. Знайдемо площу трикутника за формулою: S=½×a×h=½×8×17=4×17=68см²
Доказательство:
Будем считать, что две прямые a и b параллельны третьей прямой c. Тогда через точку M проходят две прямые a и b, которые параллельны прямой c. Это противоречит аксиоме параллельных прямых(она звучит так: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной). Следовательно, прямые a и b параллельны.