По свойству биссектрисы :
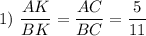
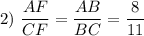
По теореме Менелая для треугольника ACF:
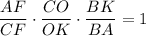
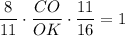
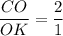
ответ: 2 : 1.
а). От 1 до 3 прямых.
б). От 1 до 6 прямых.
в). От 1 до 10 прямых.
г). От 1 до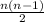 
прямых.
Объяснение:
г). [Сначала разберем общий случай] Найдем максимальное количество прямых, которое можно провести через определенные n точек, никакие три из которых не лежат на одной прямой.
Возьмем какую-нибудь точку из n точек. К скольким точкам можно провести из нее прямую? Так как никакие три из n точек не лежат на одной прямой, то всего будет сделать это. Так как это рассуждение можно сделать с любой из n точек, то мы пока получаем всего возможных сделать это: n(n-1) .
Но нужно учесть, что прямая от точки B до точки А - это тоже самое, что и прямая от точки А до точки В. Поэтому общее количество нужно разделить на 2:
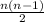
При этом можно провести любое натуральное (0 прямых не считается) число прямых меньше указанного выше числа.
а). Через три точки максимум можно провести:
(рисунок 1)
б). Для четырех точек:
(рисунок 2)
То есть, прямых можно провести любое число от 1 до 6.
в). Для пяти точек максимум равен:
(рисунок 3)
То есть, прямых можно провести любое число от 1 до 10.
То есть всего можно провести 1 прямую, 2 и 3 прямые.
Примечание:
В решении мы пользовались, тем, никакие ТРИ из прямых не лежат на одной прямой (фотография 2).
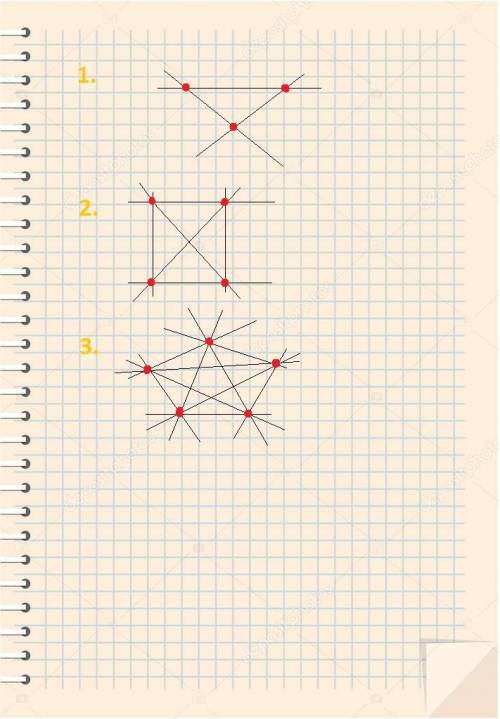
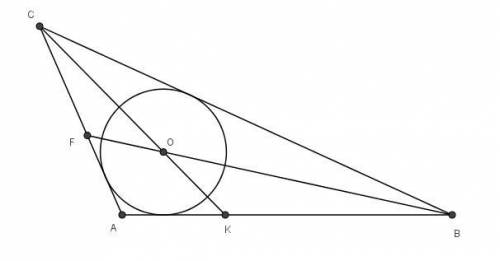
Центр вписанной окружности - точка пересечения биссектрис.
Биссектриса угла С делится точкой пересечения биссектрис в отношении (a+b)/c от вершины.
CI/IK = (AC+BC)/AB = (5+11)/8 =2/1