Объяснение:
Площадь равностороннего тр-ка:
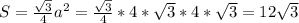
Радиус вписанной окружности:
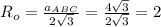
Площадь окружности:
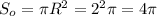
Площадь вписанного в окружность шестиугольника равна площади 6 равносторонних треугольников. сторона которых равна радиусу оуружности
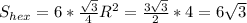
1) прямые МР и NK могут быть параллельны, т.к. углы PMN и RNM являются односторонними (в сумме дают 180градусов) и раз уж они равны, значит по 90 градусов каждый => МР II NK
так же они могут пересекаться (точка Р накладывается на точку К). И при условии, что МР=NK получаем равнобедненный треугольник с основанием МN. А углы при основании такого треугольника равны.
ответ: 5)Пересекаются или параллельны
2)
пусть один из односторонних углов х (тупой), другой y(острый), тогда:
х-y=65
x+y=180
y=180-х
х-(180-х)=65
2х=65+180=245
х=122,5градуса
y=180-122,5=57,5градусов
y - это один из острых накрест лежащих углов (накрест лежащие углы равны) =>
2y=57,5*2=115градусов
ответ: 1)115 градусов
Пусть а - сторона правильного треугольника. По условию a = 4√3 .
Тогда площадь правильного треугольника равна :
Периметр правильного треугольника равен :
P = 3 * a = 3 * 4√3 = 12√3
Радиус окружности, вписанной в правильный треугольник равен :
Сторона правильного шестиугольника равна радиусу описанной около него окружности, то есть равна 2 .
Тогда площадь правильного шестиугольника равна :