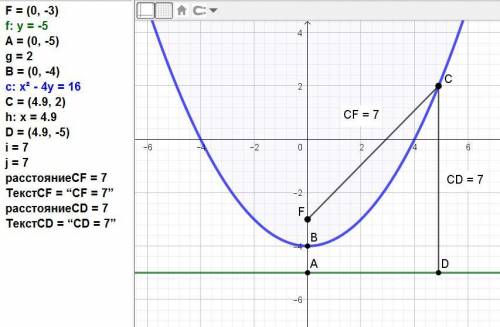
По определению заданная кривая - это парабола ветвями вверх, так директриса у = -5 находится ниже фокуса F(0;-3).
Вершина В находится посредине между фокусом и директрисой.
Её координаты: В(0; -4).
Параметр параболы р равен расстоянию от фокуса до директрисы.
р = -3 - (-5) = 2.
Отсюда определяем каноническое уравнение параболы.
x² = 2*2(у - (-4)).
Хотя это не строго каноническое уравнение - надо повернуть оси на 90 градусов вправо и поменять их обозначение, чтобы каноническое уравнение параболы выглядело так:
у² = 2*2(х - (-4)).
Задание: написать уравнение прямой ax+by+c=0, все точки которой находятся на равных расстояниях от точек A(5;2) и B(9;8) .
Геометрическое место точек, равноудалённых от точек А и В, это перпендикуляр к середине отрезка АВ.
Находим координаты точки С - середины отрезка АВ.
С = ((5+9)/2; (2+8)/2) = (7; 5).
Теперь находим уравнение прямой АВ.
Вектор АВ = (9-5; 8-2) = (4; 6). Это направляющий вектор прямой АВ.
У перпендикулярного вектора координаты такие, что скалярное произведение его и вектора прямой равно 0.
Значит, направляющий вектор перпендикуляра равен(-6; 4).
Используем координаты точки С(7; 5)..
ответ: уравнение искомой прямой (х - 7)/(-6) = (у - 5)/4 это в каноническом виде, или в общем виде 2х + 3у - 29 = 0.