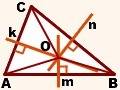
Дано:
∆ ABC,
m, n, k — серединные перпендикуляры к сторонам AB, BC, AC
Доказать: m, n, k пересекаются в одной точке.
Доказательство:
Сначала докажем, что серединные перпендикуляры к двум сторонам треугольника пересекаются в одной точке.
Предположим, что m и k не пересекаются. Тогда m ∥ k.
Но прямые AB и AC пересекаются в точке A. Пришли к противоречию. Следовательно, прямые m и k пересекаются.
Обозначим точку пересечения прямых m и k как O.
По свойству серединного перпендикуляра к отрезку AO=OC и AO=BO. Следовательно, и OC=BO. Значит, точка O равноудалена от концов отрезка BC, следовательно, лежит на серединном перпендикуляре n к этому отрезку. Таким образом, все три серединных перпендикуляра m, n, k к сторонам треугольника ABC пересекаются в одной точке O.
V=Sосн*Н
Sосн=πR², S=25π, => πR²=25π. R²=25, R=-+√25. R>0, =>
R=5 см
прямоугольный треугольник:
катет D=10 см - диаметр основания цилиндра
гипотенуза d- диагональ осевого сечения цилиндра
катет Н - высота цилиндра, найти по теореме Пифагора:
d²=R²+H²
26²=10²+H²
H²=26²-10², (26-10)*(26+10)=16*36
H=√(16*36)
H=24
V=25π*24
V=600π см²