12/5 см
Объяснение:
Пусть сторона квадрата х.
Площадь треугольника 3*12/2=18
Треугольник разбит на 3 треугольника и квадрат.
Площадь верхнего треугольника с вершиной В х*(3-х)/2
Площадь квадрата: х*х. Сумма площадей оставшихся треугольников
х*(12-х)/2. Составим уравнение
18=х*х+1,5х-0,5х*х+х*6-х*х*0,5
18=7,5х 2,5х=6 х=12/5
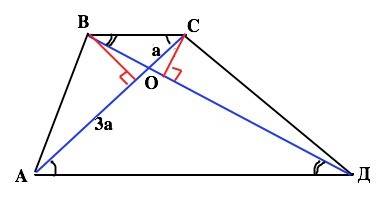
Диагонали трапеции «высекают» в ней подобные треугольники. ∆ВОС~∆ АОД по равным углам: углы при основаниях равны как накрестлежащие; при точке О - как вертикальные. k=АО:ОС=3. Отношение площадей подобных фигур равно квадрату коэффициента их подобия. ⇒ Ѕ(АОД):Ѕ(ВОС)=3²=9 ⇒ Ѕ(АОД)=36•9=324.
Высота в ∆ АВО и ВОС общая. Отношение площадей треугольников с равными высотами равно отношению сторон, к которым высоты проведены. Ѕ(АВО)=3Ѕ(ВСО)=36•3)=108 Аналогично Ѕ(СОД)=3Ѕ(ВОС)=108. (попутно заметим, что площади треугольников, образованных частями диагоналей и боковыми сторонами трапеции всегда равны именно по этому свойству). Площадь трапеции АВСД равна сумме площадей четырех треугольников. S(АВСД)=36+324+2•108=576 ( ед. площади)
Треугольники ABC и LBM подобны. BD и BE - высоты в них.
Обозначим сторону квадрата через a.
Тогда
AC/BD=LM/BE=LM/(BD-MN)
Или
16/12=a/(12-a)
откуда a=48/7