Пусть AC=x, тогда в ΔABC по формуле Герона:
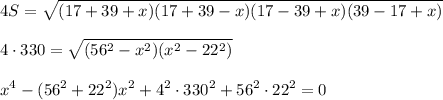
Решим квадратное уравнение относительно x².
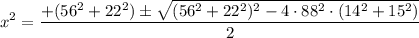
Далее немного вычислений, и зная, что x>0, как сторона треугольника, получим:
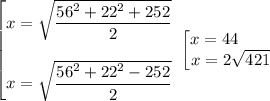
Пусть KL=a, KN=b.
Рассмотрим случай, когда AC=44.
В ΔABC по теореме косинусов:
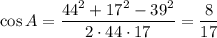
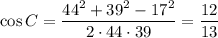
По формуле связи косинуса и тангенса:
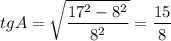
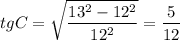
В прямоугольных треугольниках AKL и CNM выразим AK и CN через a, основываясь на определении тангенса острого угла в прямоугольном треугольнике.
AK=8a/15; CN=12a/5
AC=AK+KN+NC=(44a/15)+b=44
P(KLMN)=2a+2b=59
Составим систему и определим S(KLMN)=ab
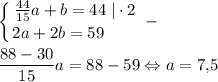
b=(59-15)/2=22
ab=7,5·22=165
Теперь всё тоже самое только AC=2√421.
В ΔABC по теореме косинусов:
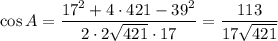
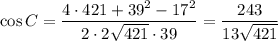
По формуле связи косинуса и тангенса:
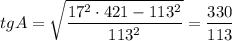
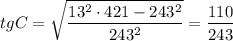
AK=113a/330; CN=243a/110
AC=AK+KN+NC=(421a/330)+b=2√421
P(KLMN)=2a+2b=59
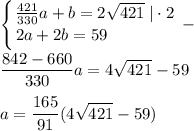
Заметим, что проекция AB на AC равна AB·cosA=113/√421
Получается, что AK=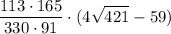 > 113/√421.
> 113/√421.
Таким образом при АС=2√421 картинка другая, которая не удовлетворяет условию задачи.
ответ: 165.
Объяснение:
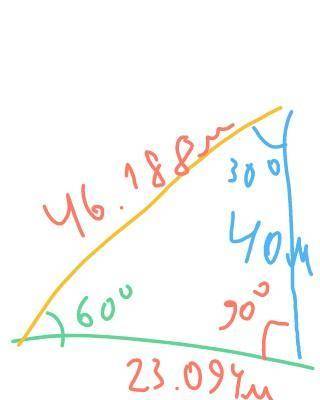
Вот рисунок, по нему решаем задачу
Видно я так понимаю самую верхушку башни под углом в 60°
Слева точка К, просто не подписал
Тогда получается прямоугольный треугольник, угол К равен 60°, правая сторона равна 40 метров
Правый верхний угол равен 30°, а сторона, лежащая напротив него равна половине гипотенузы (sin 30°=0.5)
По теореме Пифагора:
(2х)²=х²+40²
4х²-х²=1600
3х²=1600
х²=533.33
х≈23.094 - это по прямой до основания башни (зеленая линия)
23.094*2=46.188 метров - это до верхушки (желтая линия)
Проверка:
46.188²=23.094²+40²
2133.3333=533.3333+1600 - верно
ABD=90
BAC=BCA=45
Объяснение:
1) тк в равнобедренном треугольнике высота является медианой, то AD = 6.6см
2) треугольник ABD прямоугольный и в нем кареты равны => его острые углы равны 45°
3) BAC=BCA как углы при основании