У тетраэдра все ребра равны. Так как по условию, точки М, К, Р середины отрезков АВ, ВД, ВС, то отрезок КМ средняя линия треугольника АВД, КР – средняя линия треугольника ВСД, МР – средняя линия треугольника АВС.
Отрезки средних линий параллельны основаниям треугольников: MK || АД, КР || СД, МР || АС, тогда и плоскость МКР параллельны плоскости АСД, что и требовалось доказать.
Длина средней линии треугольника равна половине длины параллельной стороны, тогда треугольник МКР подобен треугольнику АСД по трем пропорциональным сторонам с коэффициентом подобия К = АД / МК = АД / (АД / 2) = 2.
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Sавс / Sмкр = 48 / Sмкр = 22.
Sмкр = 48 / 4 = 12 см2.
ответ: Площадь треугольника МКР равна 12 см2.
Объяснение: правильно? ;-;

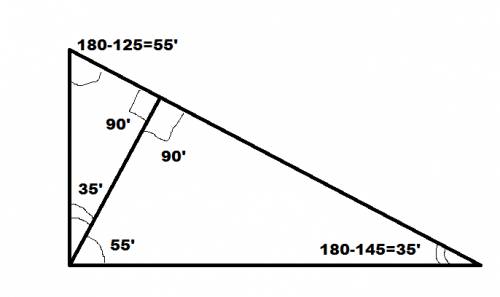
На гипотенузе при высоте каждый угол равен 90'
Так как треугольник прямоугольный, можно сказать, что, если разделить его прямой угол на две части, одна из которых будет равна 55, то вторая будет равна 35 градусам.
У нас получилось два маленьких прямоугольных треугольника в одном большом. Сумма углов любого треугольника равна 180 градусов, следовательно, третий угол в маленьком нижнем треугольнике на картинке будет равен 180-(55+90)=35 градусов.
Острые углы — это все углы меньше 90 градусов.
Так как угол 45 градусов , то и высота равна 10
V=Sосн*H
Socн=pi*R^2=25pi
V=25pi*10=250pi