Сумма острых углов прямоугольного треугольника 90°. Поэтому сумма их половин равна 45°, и величина углов, образуемых их биссектрисами, всегда будет 45° и 135°.
По условию угол, образуемый биссектрисами, равен 70°, следовательно, одна из биссектрис проведена из прямого угла.
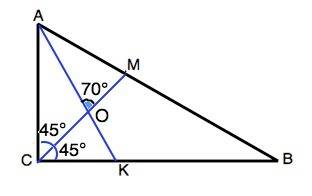
Обозначим вершины треугольника А, В, С. Биссектрисы СМ и АК. Точка пересечения биссектрис О.
∠МОА=70°
∠ОСА=45°.
∠МОА - внешний для ∆ СОА и равен сумме внутренних не смежных с ним углов. ⇒
∠ОАС=70°- 45°=25°⇒
∠ВАС=2•25°=50°
∠АВС=90°-50°=40°.
ответ: 50° и 40°.
Сумма острых углов в прямоугольном треугольнике 90 градусов, поэтому сумма их половин 45 градусов, и углы между биссектрисами острых углов будут 45 градусов и 135 (ну, там 4 угла, пары вертикальных... в сумме 180, конечно). Значит, речь идет не о двух острых углах, а о прямом и остром.
Тем же определяем, что углы между биссектрисами прямого и острого угла Ф равны Ф/2 + 45 градусов и 135 - Ф/2 градусов.
в первом случае Ф =2*(70 - 45) = 50 градусов, а второй угол треугольника 90 - Ф = 40 градусов.
Во втором случае 135 - Ф/2 = 70 просто получается Ф > 90.
То есть ответ 40 и 50 (третий угол 90, конечно), в таком треугольнике биссектрисы углов 90 градусов и 50 градусов пересекаются под углом 70 градусов.
8 см
Объяснение:
Дано: КМРТ - трапеция, МР=6 см, КТ=8 см, КМ=РТ=4 см. Найти КР.
Проведем высоты МС = РН. СН=МР=6 см. ΔКМС=ΔТРН по катету и гипотенузе, значит КС=ТН=(8-6):2=1 см.
Найдем РН из ΔТРН по теореме Пифагора:
РН=√(РТ²-ТН²)=√(16-1)=√15 см.
ΔКРН - прямоугольный, КН=КС+СН=6+1=7 см. По теореме Пифагора КР=√(КН²+РН²)=√(49+15)=√64=8 см.