Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:
S = (1/2)ah, где а - основание, а h - высота.
Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна . Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
S = (1/2)*3*8 = 12.
Следовательно, площадь данного треугольника равна 12 (номер ответа - 3).
Рассмотрим треугольник МРВ. В нем МР=РВ и уг.МРВ=гр по условию. Значит этот треугольн-и)/равнобедренный и углы при основании МВ равны. т.е. уг.ВМР=уг.РВМ=(180-60)/2=60гр. получается все углы равны, значит треугольник равносторонний. Таким образом: уг.НМР=уг.НКР=60гр. - противолежащие углы параллелограмма. сумма углов прилежащих к одной стороне =180гр. уг.КРМ=уг.КНМ= 180-60=120гр. Рассмотрим треуг. АКН. КН=РМ- противоположные стороны параллелограмма АК=КН т. к. АК=РМ по условию. Значит треугольник равнобедренный уг.КАН=уг.КНА=(180-60)/2=60гр. Раз все углы треугольника равны, значит треуг.АКН-равносторонний и АН=АК. Т. к. АК=ВМ-по условию, то и АН=ВМ.
ответ: 3) 12.
Итак, у нас есть равнобедренный треугольник со сторонами 5, 5, 8. И нужно найти его площадь. Например, по формуле:
S = (1/2)ah, где а - основание, а h - высота.
Но высоту мы не знаем. Попробуем ее найти. В предлагающемся ниже рисунке видно, что можно разделить этот треугольник на два прямоугольных одинаковых треугольника, у каждого из которых основание по 8/2 = 4, а гипотенуза - 5. Поэтому общая высота, по теореме Пифагора (сумма квадратов равна квадрату гипотенузы), равна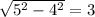 . Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
. Теперь, когда мы знаем и высоту, и основание, мы сможем найти площадь:
S = (1/2)*3*8 = 12.
Следовательно, площадь данного треугольника равна 12 (номер ответа - 3).