ответ: во вложении Объяснение:

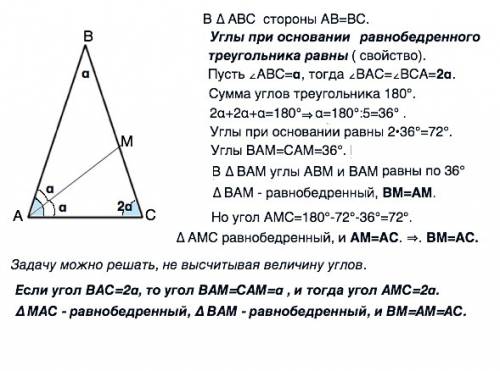
В ∆ АВС стороны АВ=ВС. Углы при основании равнобедренного треугольника равны ( свойство).
Пусть ∠АВС=α, тогда ∠ВАС=∠ВСА=2α.
Сумма углов треугольника 180°. 2α+2α+α=180° α=180°:5=36° .
Углы при основании равны 2•36°=72°.
Углы ВАМ=САМ=36°. В ∆ ВАМ углы АВМ и ВАМ равны по 36°.
∆ ВАМ - равнобедренный, ВМ=АМ.
Но угол АМС=180°-72°-36°=72°.
∆ АМС равнобедренный, и АМ=АС. ⇒. ВМ=АС.
-------
Задачу можно решать, не высчитывая величину углов.
Если угол ВАС=2α, то угол ВАМ=САМ=α , и тогда угол АМС=2α.
∆ МАС - равнобедренный, ∆ ВАМ - равнобедренный, и ВМ=АМ=АС.
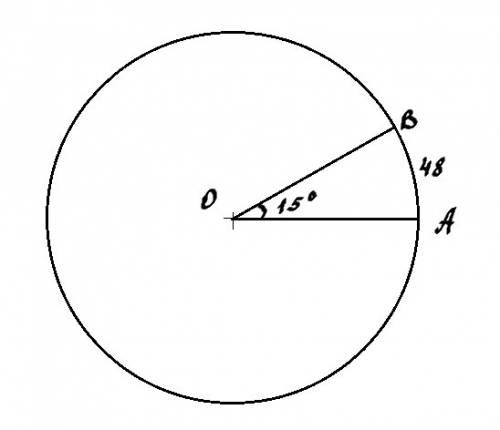
Угол АОВ центральный (смотри рисунок). Его градусная мера равна градусной мере дуги, на которую он опирается.
Малая дуга АВ равна 15°. Длина же ее равна 48.
Решим задачу, используя отношение.
Во сколько раз градусная мера большой дуги АВ больше градусной меры малой дуги АВ, во столько же раз длина большой дуги АВ больше длины малой дуги АВ.
Градусная мера всей окружности 360°.
360°–15° = 345° – градусная мера большой дуги АВ.
345°:15° = 23.
В 23 раза градусная мера большой дуги АВ больше градусной меры малой дуги АВ.
48*23 = 1104 – длина большой дуги АВ.
ответ: 1104.
2 см.
Объяснение:
Проведем высоту СН, тогда АН=ВС=DН=х см
АН=DН, СН - высота и медиана, значит ΔАСD - равнобедренный и АС=СD=2 см.