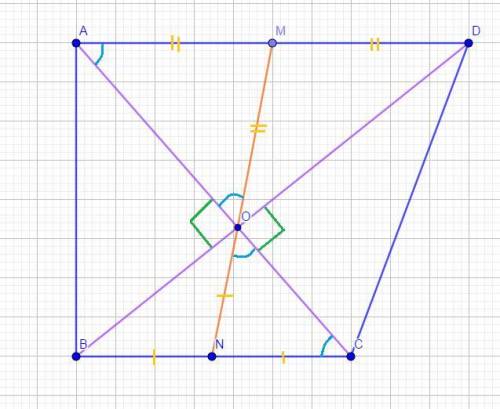
Четырехугольник ABCD, O - точка пересечения диагоналей,
AD || BC и AC ⊥BD,
M - середина AD, N - середина BC,
AD = 12 и BC = 7 (смотрите рисунок).
Найти:Длина отрезка MN.
Решение:Заметим, что O ∈ MN, так как угол MON - развернутый:
∠MON = ∠DOC + (∠DOM + ∠CON) = 90° + (∠OCB + ∠OBC) =
= 90° + 90° = 180°.
Значит, нам достаточно найти длину MO + NO.
Так как треугольник AOD прямоугольный, то медиана MO, проведенная из вершины прямого угла к гипотенузе, равна половине этой гипотенузы (по свойству медианы прямоугольного треугольника):
MO = AD / 2 = 12 / 2 = 6.
Тоже самое можно сказать и о прямоугольном треугольнике BOC с медианой NO:
NO = BC / 2 = 7 / 2 = 3,5.
Значит:
MO + NO = MN = 6 + 3,5 = 9,5.
ответ:MN = 9,5 .
ответ:1) 57°, 70° и 53°. 2) 35° и 55°.
Объяснение:
1)Пусть высота проведена из угла М, тогда МН⊥КN.
∠М=20°+37°=57°.
ΔКМН: ∠Н=90°, ∠К=90°-20°=70° из теоремы
о сумме углов треугольника.
ΔМNН: ∠МНN=90°, ∠N=90°-37°=53° из теоремы
о сумме углов треугольника. .
ответ: 57°, 70° и 53°.
2)Пусть в ΔАВС ∠В=90° и ВК- биссектриса, ∠АКВ=80°, тогда:
∠АВК=КВС=45° по свойству биссектрисы угла.
ΔАВК: ∠А=180°-(∠АВК+∠АКВ)=180°-(45°+80°)=180°-125°=55°.
∠С=90-∠А=90°-55°=35°.
ответ: 35° и 55°.