Биссектриса равностороннего треугольника является медианой и высотой. Обозначим сторону треугольника буквой х.
Биссектриса равностороннего треугольника разбивает его на два равных прямоугольных треугольника, гипотенуза треугольника равна х, биссектриса является одним катетом, длина второго катета равна х/2.
По теореме Пифагора: х² = (x/2)² + (12√3)².
х² = x²/4 + 144 * 3.
х² - x²/4 = 432.
(4х²)/4 - x²/4 = 432.
(3х²)/4 = 432.
3х² = 432 * 4;
3х² = 1728;
х² = 1728/3 = 576.
х = √576 = 24.
ответ: сторона треугольника равна 24.
Объяснение:
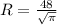
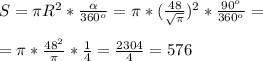
Угол С равен 30°, поскольку катет АВ противолежащий ему, равен половине гипотенузы, а угол А соответственно 60°.
Высота из прямого угла делит прямоугольный треугольник на два треугольника, подобных исходному, имеющих с исходным по общему острому углу.
Сумма острых углов прямоугольного треугольника 90°.
В прямоугольном ∆ АВН угол А=60°,⇒
ВН образует с катетом АВ угол АВН=90°- 60°= 30°.
В ∆ ВНС высота ВН образует с катетом ВС угол СВН=90°-30°=60°, т.к. угол С=30