Объяснение:
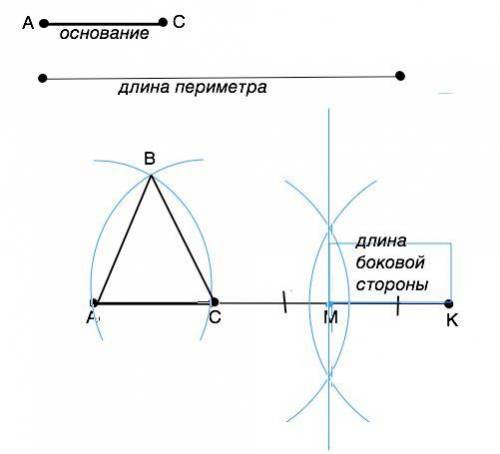
1) На произвольной прямой отложить отрезок, равный длине периметра. Обозначить его АК.
2) От т.А циркулем отметить на АК точку С, АС= длине данного основания.
3). Отрезок СК разделить на две равные части. Для этого из т.С и т.В провести две полуокружности до их пересечения по обе стороны от СК. Точки пересечения соединить прямой ( срединным перпендикуляром). Точку пересечения этой прямой и отрезка СК обозначить М. СМ=МК=длина боковой стороны треугольника.
4). Циркулем с раствором, равным МК, провести из точек А и С дуги до их пересечения. Точку пересечения обозначить В и соединить с т.А и т.С. Треугольник АВС - искомый.
1. на 1 картинке, ответ Б
2. Т.к. угол А = 30°, CF = 1/2 AC.
CF = 16÷2 = 8
По теореме Пифагора
AF^2 = 16^2-8^2 = 256 - 64 = 192
AF = √(192) = 8√(3)
Т.к. АСК - равнобедренный треугольник, СF - биссектриса, медиана и высота.
То есть, AF = 1/2 AK
AK = 8√(3)×2 = 16√(3)
ответ А
3. Картинка 2
Т.к. 2 угла в треугольнике = 60° и 90°, 3 угол - 30° (острый)
Т.к. противолежащий катет угла 30° = 14,
АС = 2×14 = 28 (гипотенуза)
По теореме Пифагора
АВ^2 = АС^2-ВС^2
АВ^2 = 28^2-14^2 = 784-196 = 588
АВ = √(588) = 14√(3).