Объяснение:
Т.к. угол MPH=45 то треугольник MPH равнобедренный т.е. PH=MH=7, а MP=7корень2
S=1/2×ab×sina
S=59.5
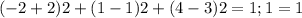, значит точка А(-2; 1; 4) Лежит на сфере, заданной уравнением (x+2)2+(y-1)2+(z-3)2=1.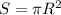 
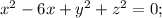
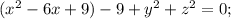
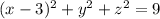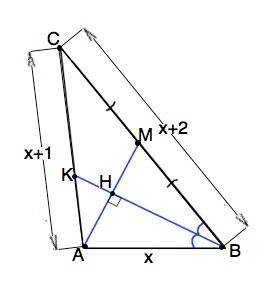
- уравнение окружности
Обозначим медиану АМ, биссектрису ВК.
ВК⊥АМ и пересекает ее в т.Н.
ВН является высотой ∆ АВМ.
Высота и биссектриса совпадают ⇒ треугольник АВМ равнобедренный, ВМ=АВ
Длины сторон треугольника ABC — последовательные целые числа (дано).
Примем сторону АВ=х, АС=х+1, ВС=х+2
Тогда СМ=х+2-х=2
Т.к. АМ медиана, то ВМ=СМ=2, ⇒
ВС=4, АВ=ВМ=2, АС=2+1=3
Предположим, что большей является сторона АС. Тогда АВ=1, ВС=2, АС=3; это противоречит теореме о неравенстве треугольника (3=1+2). Следовательно, АВ=2, АС=3, ВС=4
Периметр АВС=2+3+4=9 (ед. длины)
Объяснение:
1)S=0,5*РН*МК
2)ΔМРН-прямоугольный , т.к. РН⊥МК. Найдем ∠РМН=90-45=45, по свойству острых углов прямоугольного треугольника. Значит ΔМРН-прямоугольный и равнобедренный, поэтому РН=МН=7 (см)
3)МК=7+10=17
4) S=0,5*7*17=59,5 ( см²)