СРАЗУ ОТВЕТЫ!!)) :
1) ответ: Да
2) ответ: Нет
3) ответ: Нет
4) ответ: 1 < x < 9
5) ответ: 3 < x < 11
6) ответ: 0 < x < 2a
7) ответ: x > a/2
8) ответ: 1 < x < 5
9) ответ: 1 < x < 2.2
Подробное обьяснение:
1 - 3)
Для первых трёх заданий сделаем утверждение:
ΔABC существует тогда, когда сумма двух его любых сторон строго больше оставшейся третьей. Составим систему уравнений:
AC + BC > AB
AB + AC > BC
AB + BC > AC
Если для любого треугольника ABC не выполняется эта система, такого треугольника не существует.
1)
3 + 5 > 6
3 + 6 > 5
5 + 6 > 3
8 > 6
9 > 5
11 > 3
Система выполняется, => существует.
1) ответ: Да
2)
4 + 5 > 10
9 > 10
Для других сторон даже не надо вычислять, сразу видно, что такого треугольника не существует.
2) ответ: Нет
3)
Составим систему уравнений отдельно для этого треугольника, взяв из основной системы второе уравнение:
AB + 7 > BC
AB - BC = 10
Из второго уравнения, BC = AB + 10.
AB + 7 > AB + 10
Отнимаем от обеих частей уравнения AB:
7 > 10
Неравенство не выполняется => не существует
3) ответ: Нет
4 - 9) Здесь немного другое условие и другой метод решения, но система остаётся.
4)
4 + 5 > x
4 + x > 5
5 + x > 4
Переносим все числа в правую часть.
x < 9
x > 1
x > -1
Нас интересуют первые два неравенства. Они и задают интервал x.
4) ответ: 1 < x < 9
5) AD медиана, т.е. BD = 8/2 = 4
Рассмотрим треугольник ABD. Составим для него систему:
7 + 4 > x
7 + x > 4
4 + x > 7
x < 11
x > -3
x > 3
5) ответ: 3 < x < 11
6) Не пугаемся того, что здесь нет чисел, машинально строим нашу любимую систему:
a + a > x
a + x > a
a + x > a
Убираем третье уравнение - оно повторяет второе. Переносим все a направо, x налево.
x < 2a
x > 0
6) ответ: 0 < x < 2a
7)
x + x > a
x + a > x
Я сразу убрал третье уравнение.
x > a/2
a > 0
На самом деле, нам не нужно и второе уравнение (понятное дело что не бывает нулевых и отрицательных сторон). Важно первое. В этом треугольнике x может быть сколько угодно большим, главное чтобы больше половины a (если не верите, попробуйте сами нарисовать равнобедренный треугольник с крошечным основанием и длиннющими боковыми сторонами, это будет похоже на меч). Поэтому:
7) ответ: x > a/2
8) Для начала найдём границы AB:
4 + 6 > AB
4 + AB > 6
6 + AB > 4
AB < 10
AB > 2
AB > -2
То есть интервал AB: 2 < AB < 10
Если интервал AB это 2 < AB < 10; а AD половина AB, то интервал AD - половина интервала AB:
1 < AD < 5.
Рассмотрим треугольники ADC и BDC.
Обозначим AD = BD = a
Найдём границы x в обеих треугольниках.
В тр. ADC:
a + x > 6
x + 6 > a
a + 6 > x
x > 6 - a
x > a - 6
x < a + 6
Нам нужны последние два неравенства.
В тр. BDC:
a + x > 4
x + 4 > a
a + 4 > x
x > 4 - a
x > a - 4
x < a + 4
Опять же, берем второе и третье неравенство.
Составим систему из пяти неравенств:
x > a - 6
x < a + 6
x > a - 4
x < a + 4
1 < a < 5
Избавимся от лишних неравенств. Мы знаем, что (a - 4) > (a - 6), поэтому смело избавляемся от первого уравнения, третьего достаточно. Таким же избавляемся от второго уравнения, (a + 6) > (a + 4), если x меньше какого-то числа, то понятно что оно меньше чисел больше. Итак:
x > a - 4
x < a + 4
1 < a < 5
Подставляем в первые уравнения верхнюю и нижнюю границу a:
x > 1 - 4
x > -3
x > 5 - 4
x > 1
x < 1 + 4
x < 5
x < 5 + 4
x < 9
8) ответ: 1 < x < 5
9) Мне кажется, для вас после 8 задания это вообще легче лёгкого:
0.6 + 1.6 > x
0.6 + x > 1.6
1.6 + x > 0.6
x < 2.2
x > -1
x > 1
9) ответ: 1 < x < 2.2
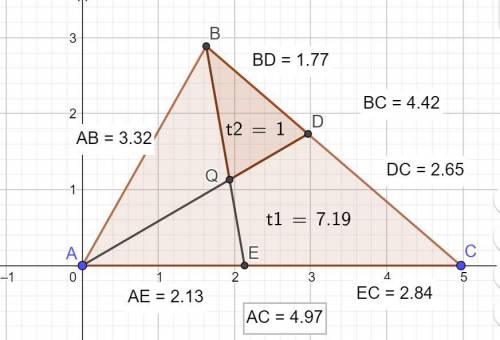
Из заданного соотношения длин сторон треугольника АВС имеем:
АВ = 1, АС = (3/2)АВ, ВС = (4/3)АВ.
Приводим к общему знаменателю и представляем длины сторон подобного треугольника в целом виде: А1В1 = 6, А1С1 = 9, В1С1 = 8.
Находим углы этого (они же и у заданного) треугольника по теореме косинусов : cosα = (b²+c²−a²)/2bc.
Подставив данные длин сторон треугольника А1В1С1, находим:
cos A = 0,490741,
cos B = 0,1979167,
cos C = 0,756944.
Соответственно углы равны:
A = 1,057857 радиан или 60,61072 градусов,
B = 1,371564 78,584842,
C = 0,712172 40,804438.
Отсюда находим угол Q1D1B1 по сумме углов смежного треугольника: ∠Q1D1B1 = (1/2)∠А + ∠С = 71,109798 градуса.
Теперь переходим к длинам треугольника Q1D1B1.
Длина B1D1 по свойству биссектрисы р = ((ас)/(b + c)) равна:
B1D1 = p = (8*6)/(9 + 6) = 48/15 = 16/5 = 3,2.
Отрезок С1D1 = q = 8 - 3,2 = 4,8.
Находим длину биссектрисы А1D1:
A1D1 = √(bc - pq) = √(9*6 - 3,2*4,8) = √38,64 ≈ 6,216108.
Биссектриса А1D1 делится точкой пересечения с биссектрисой В1Е1 в отношении (b + c)/a. Отсюда находим длину Q1D1.
Q1D1 = A1D1*(a/(a + b +c)) = 6,216108*(8/23) = 2,162125.
Теперь можно определить площадь подобного треугольника Q1D1B1 по двум сторонам и углу между ними.
S(Q1B1D1) = (1/2)*2,162125*3,2*sin71,109798° = 3,273079.
Находим коэффициент"к" пропорциональности треугольников QBD и Q1B1D1:
к =√(S(QBD)/S(Q1B1D1)) = √(1/3,273079) = 0,552741.
По этому же коэффициенту находим длины сторон треугольника АВС.
Площадь АВС = 7,1875 А1В1 = В1С1 = А1С1 = Р = 12,713046
AB =3,316447
BC =4,421929
AC =4,974670/
Площадь АВС находим по формуле Герона.
Р = 12,713046, р = 6,356523.
S(АВС) = 7,1875 кв.ед.
Проверяем соотношение длин сторон:
1 1,3333 1,5
1 4/3 3/2. Соответствует заданному.
ответ: площадь АВС = 7,1875 кв.ед.
4. Дан ромб ABCD.Выразите векторы BD и СA через AB и СD .
4. Дан ромб ABCD.Выразите векторы BD и СA через AB и СD
Задача с недостающими данными.
СD ничего не прибавляет к условию ( СD = - AB )
Поэтому , допустим СD задан вектор BC
BD = BA +AD = - AB + BC ; CA = CB + BA = - BC - AB = - ( AB +BC ) .
или коротко CA = - AC = - (AB +BC ) .
- - - - - - - - - - - - - - -
5. Дано: a(1 ; - 4) и b(3 ; -1) . Найдите 3a - 2b .
a = i - 4j ; b =3i -j ; 3a - 2b =3( i - 4j ) -2(3i -j) =3i -12j -6i+2j = -3i -10j .
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3a (3*1 ; 3(-4) ) ⇔ 3a (3 ; -12 ) ; -2b (-2*3 ; -2*(-1) ) ⇔ - 2b (- 6 ;2 )
3a - 2b = 3a +(- 2b) ( 3 - 6 ; - 12+2 ) 3a - 2b ( - 3 ; - 10 )
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
2b(2*3 ; 2*(-1) ) ⇔2b(6 ; -2 ) ; - 2b( -6 ; 2 )
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Объяснение:
решение в приложении