ответ: Р=36 см .
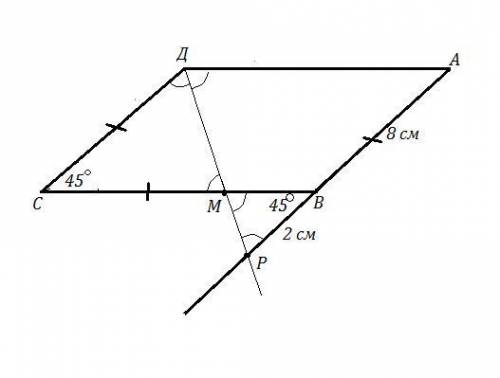
АВСД - параллелограмм , ДР - биссектриса, ∠С=45° ,
ДР пересекает АВ в точке Р , а ВС в точке М .
АР=10 см , ВР=2 см ⇒ АВ=10-2=8 см , СД=АВ=8 см как противоположные стороны параллелограмма .
ДР - биссектриса ⇒ ∠СДР=∠АДР .
∠АДР=∠СМД как накрест лежащие углы при АД || ВС и секущей ДР .
В ΔСМД два угла равны ⇒ ΔСМД - равнобедренный и СМ=СД=8 см ∠СМД=(180°-45°):2=67,5°
∠ВМР=∠СМД=67,5° как вертикальные .
В ΔВМР угол ∠МВР=45° , так как ∠МВР=∠МСД=45° как накрест лежащие углы при АР || СД и секущей ВС .
Но тогда в ΔВМР: ∠ВРМ=180°-45°-67,5°=67,5° , то есть ΔВМР есть два равных угла: ∠ВМР=∠ВРМ=67,5° , тогда этот треугольник равнобедрен-ный и ВМ=ВР=2 см .
Тогда ВС=СМ+ВМ=8 +2 =10 см , АД=ВС=10 см
Периметр Р=10+10+8+8=36 см .
РЕШЕНИЕ
стороны основания a=3 b=5
острый угол основания A=60 град
тупой угол основания B=180-60=120 град
площадь основания Sо=ab*sinA = 3*5*sin60=15√3/2 см2 <--- два основания
большая диагональ основания -по теореме косинусов
d^2=a^2+b^2 - 2ab*cosB = 3^2+5^2 -2*3*5*cos120=49
d =7 см
площадь большого диагонального сечения равна Sc=d*h <---h -высота
h=Sc / d = 63 / 7=9 см
периметр P=2*(a+b) = 2*(3+5) = 16 см
площадь боковой поверхности Sбок= P*h = 16*9=144 см2
ПЛОЩАДЬ ПОЛНОЙ ПОВЕРХНОСТИ
Sпп = 2*So + Sбок = 2*15√3/2 + 144 = 15√3 + 144 см2
ОТВЕТ
15√3 + 144 см2
или
144+15√3 см2
AC=15 см
Объяснение: