1. ∠АВС = 65°.
2. ∠АВС = 115°.
Объяснение:
Расположение точки В нам неизвестно, но предполагаем, что она находится на окружности.
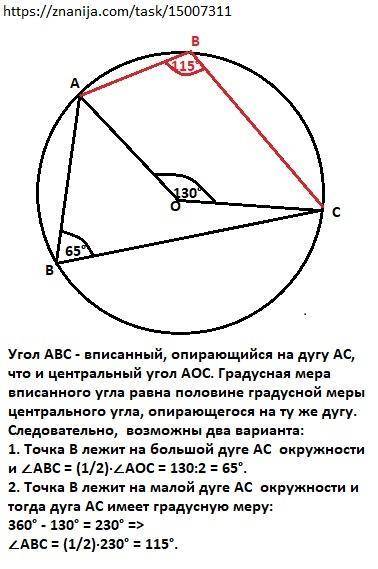
Угол АВС - вписанный, опирающийся на дугу АС, что и центральный угол АОС. Градусная мера вписанного угла равна половине градусной меры центрального угла, опирающегося на ту же дугу. Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Следовательно, возможны два варианта:
1. Точка В лежит на большой дуге АС окружности и
∠АВС = (1/2)·∠АОС = 130:2 = 65°.
2. Точка В лежит на малой дуге АС окружности и тогда дуга АС имеет градусную меру:
360° - 130° = 230° =>
∠АВС = (1/2)·230° = 115°.
am=cm=a1m1=c1m1.
Рассмотрим треугольники abm и a1b1m1. Они равны по трем сторонам:
- ab=a1b1 по условию;
- bm=b1m1 по условию;
- am=a1m1 как только что доказано.
У равных треугольников abm и a1b1m1 равны соответственные углы amb и a1m1b1. Значит, углы bmc и b1m1c1, равные 180-<amb и 180-<a1m1b1, также равны между собой.
Треугольники bmc и b1m1c1 будут равны по двум сторонам и углу между ними:
- bm=b1m1 по условию;
- сm=c1m1 как было показано выше;
- углы bmc и b1m1c1 равны как доказано выше.
У равных треугольников bmc и b1m1c1 равны соответственные стороны bc и b1c1.
Таким образом, треугольники abc и a1b1c1 получаются равными по трем сторонам.