1) Через две различнье точки всегда можно провести окружность.
ДА
2) Через две различные точки всегда можно провести окружность , и притом только одну.
НЕТ, окружностей бесконечно много.
3) Через две различные точки всегда можно провести окружность данного радиуса.
НЕТ, если расстояние меж точками больше диаметра окружности - то её не построить
4) Через две различные точки всегда можно провести окружность радиуса, paвного между этими точками , и притом только одну.
Ошибка в вопросе!
Если расстояние меж точками = диаметру окружности - то да, её можно построить только одну.
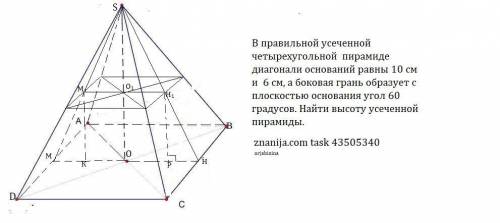
В правильной усеченной четырехугольной пирамиде диагонали оснований равны 10 см и 6 см, а боковая грань образует с плоскостью основания угол 60 градусов. Найти высоту усеченной пирамиды.
Объяснение:
1) АВСDA₁B₁C₁D₁- усеченная пирамида , Точки О и О₁ -точки пересечения диагоналей оснований Т.к пирамида правильная , то основания кавдраты.
АВСD- нижнее основание , по т. Пифагора АВ=√(10²:2)=5√2 (см).
A₁B₁C₁D₁-верхнее основание , по т. Пифагора A₁B₁=√(6²:2)=3√2 (см).
2) Проведем через точки О и О₁ отрезки МН и М₁Н₁ перпендикулярно сторонам квадратов.Тк О₁Н₁ ⊥ВС, то SH⊥ВС по т. о трех перпендикулярах . Поэтому линейным углом между плоскостью боковой грани и плоскостью основания будет ∠НН₁М=60°.
3) Рассмотрим сечение , проходящее через МН и М₁Н₁ перпендикулярно сторонам основаниям. В сечении получилась равнобедренная трапеция ММ₁Н₁Н.
Проведем высоты М₁К и Н₁Р в трапеции . Тогда КР=М₁Н₁ =3√2 см , а МК=РН=( 5√2-3√2):2=√2 (см).
ΔРНН₁ -прямоугольный , tg60°=PН₁ /PH , √3=PН₁ /√2 , PН₁ =√6 см.
Поэтому высота усеченной пирамиды √6 см.
Квадрат - четырёхугольник, стороны которого равны между собой.
Обозначим сторону за a.
Площадь квадрата(S) найдём по формуле S=a². Получим:
a²=4
a1=2 или a2=-2(не удовлетворяет условию задачи)
Следовательно сторона квадрата(a)=2 см.
ответ:2см.