4.Т.к. треугольник равнобедренный, ТО УГЛЫ ПРИ ОСНОВАНИИ ОР равны, значит, и угол Р равен 30°, тогда угол Н равен 180°-60°=120°.
6. Т.к. треугольник равносторонний у него все углы по 60°.
8. Т.к. треугольник равнобедренный,ТО ВНЕШНИЙ угол при вершине С равен сумме двух внутренних, не смежных с ним, т.е. равен 40°+40°=80°, тогда внутренний угол С равен 180°-100°=80°, по свойству смежных.
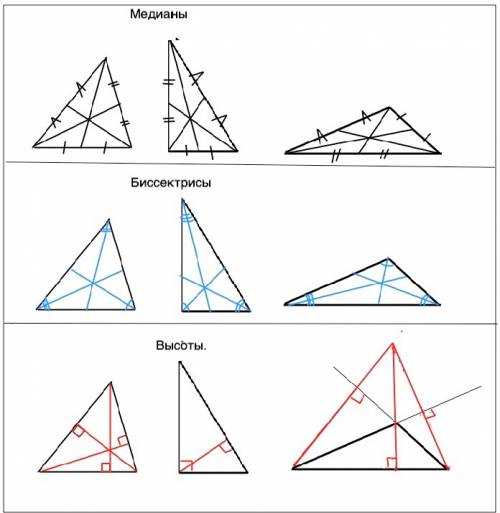
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
№1
Найдем гипотенузу AB
AB= 3√3 : √3/2=6
Найдем BC
По теореме Пифагора:
36-27=9 BC=3
ответ: 3
№2
треугольники CHB и CHA
Из треугольника CHB найдем СH.
Так как тругольник ABC ранвостороний, то точка H делит AB на две равные отрезки (AH=HB) HB= 2√2/2= √2
По теореме Пифагора:
CH^2 + (√2)^2=(2√2)^2
CH=√6
ответ: √6
№3
ABCD-ромб, точка О- точка пересечения диагоналей.
Так как угол АВС=60 градусов, то угол ОВС=30 градусов
Из треугольника BOC
ВО=19* cos30 градусов=19 * √3/2= 9,5√3
По теореме Пифагора найдем OC
OC^2=361-270,75=90,25 OC=9,5
AС-меньшая диагональ ромба
AC=2OC
AC=2*9,5=19
ответ: 19
4.) OPN = PON = 30°
ONP = 180-(30+30) = 120°
6.) Т.к. треугольник равносторонний, все углы = 60° (180÷3 = 60°)
7.) АСВ = 180-(40+40) = 100°
АСЕ = 180-100 = 80°