Возьмём любое боковое ребро наклонной призмы. Из одной вершины (1) опустим перпендикуляр на плоскость основания, в котором лежит другая вершина (2). Соединим основание перпендикуляра с другой вершиной (2).
Получили прямоугольный треугольник (перпендикуляр к плоскости основания будет перпендикулярен люб(ой/ому) прямой/отрезку, лежащ(ей/ему) в плоскости этого основания) с катетом, являющимся высотой призмы, и острым углом в 30° (т.к. это и есть угол между боковым ребром и его проекции на основание), лежащим напротив этого катета. Гипотенузой будет боковое ребром. Катет лежащий напротив угла в 30°, в прямоугольном треугольнике, равен половине гипотенузы, то есть высота наклонной призмы равна 12см:2 = 6см.
ответ: 6см.
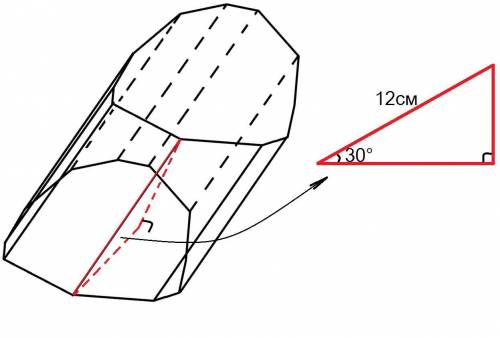
как-то так ... ... ... ... ...