решение представлено на фото
Объяснение:


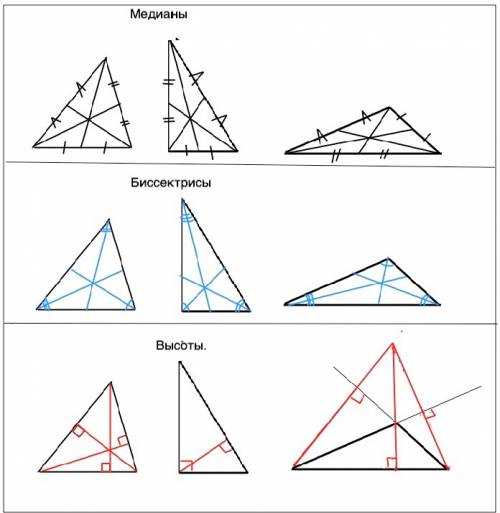
Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2:1, считая от вершины.
Биссектрисы треугольника пересекаются в одной точке, расстояние от которой до сторон треугольника одинаково и является центром вписанной окружности.
Высоты треугольника пересекаются в одной точке. Точка пересечения высот остроугольного треугольника находится внутри него. Точка пересечения высот прямоугольного треугольника - вершина прямого угла.
Высоты тупоугольного треугольника, проведенные из вершин его острых углов, проходят вне его и пересекают продолжения сторон. Точка пересечения высот тупоугольного треугольника находится вне треугольника.
y = 1 - 2x
у(1) = 1 - 2 · 1 = 1 - 2 = -1;
у(-1) = 1 - 2 · (-1) = 1 + 2 = 3;
у(2) = 1 - 2 · 2 = 1 - 4 = -3;
у(-2) = 1 - 2 · (-2) = 1 + 4 = 5.
Наименьшим из полученных чисел будет число у(2) = -3.
ответ: -3.