Высота QL делит тр-к PQR на два подобных треугольника: QRL и PQL. Эти прямоугольные тр-ки подобны по двум равным углам: уг.QRL = уг.PQL и уг.RQL = уг.QPL как острые углы с взаимно перпендикулярными сторонами. Эти тр-ки подобны также и исходному тр-ку PQR по тем же углам.
Против равных углов в подобных тр-ках лежат пропорциональные стороны:
Катет PQ в тр-ке PQR и катет PL в тр-ке PQL лежат против равных углов (уг.QRL = уг.PQL), гипотенуза PR в тр-ке PQR и гипотенуза PQ в тр-ке PQL лежат (естественно!) против прямых углов, поэтому
PQ:PL = PR:PQ: ,
откуда
PQ^2 = PL * PR.
2,5
Объяснение:
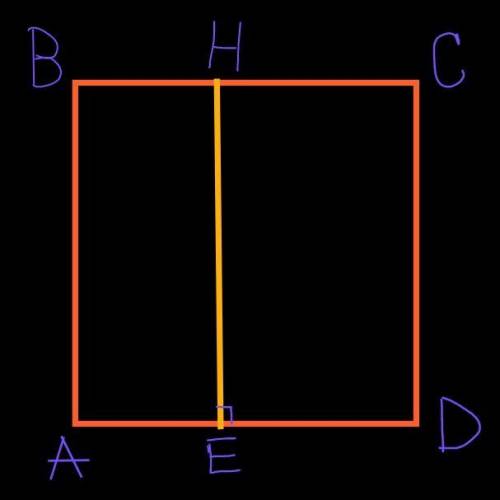
Назовём точки как на рисунке.
Пусть периметр прямоугольника АВНЕ равен 7.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника. Следовательно а+б=P÷2; тоесть АВ+АЕ=7÷2; АВ+АЕ=3,5
Пусть периметр прямоугольника CDEH равен 8.
P(прямоугольника)=(а+б)*2,
где а и б стороны прямоугольника
Следовательно а+б=P÷2; тоесть CD+DE=8÷2; CD+DE=4.
АЕ+DE=AD. Тогда АВ+АD+CD=3,5+4=7,5.
АВ, AD и CD – стороны квадрата ABCD
Все стороны квадрата равны, следовательно одна сторона равна 7,5÷3=2,5
ответ: 2,5